区块链技术探索(一), 构造比特币的创世区块
0. 从一种更简单的角度理解区块链技术
如果我们使用搜索引擎去搜索 区块链, 我们看到最多的是 去中心化, 分布式, 信任, 不可更改, 不可伪造, 共识, 工作量证明, POW, 权益证明, POS, 公链, 私链, 联盟链, 智能合约, 未来 等等一堆类似的词汇。
现在让我们将这些词汇从大脑中一个个剔除掉,让我们对区块链的认识归零。
传统中心和区块链的矿工
在传统的中心化应用里, 中心需要做很多繁杂的事情, 而在比特币世界里, 矿工只做三件事情: 1.验证交易 2.记录交易 3.读交易, 当然为了做成这三件事情,矿工需要做很多其他幕后的工作。
在传统的中心化应用里, 中心接收你的命令,为你完成相关的任务, 而在比特币世界里, 矿工只做三件事情: 1.验证交易 2.记录交易 3.读交易, 矿工不会接受你的任何命令。
在传统的中心化应用里, 中心即使没有你的命令,也可以为你完成意想不到的任务,比如将你的帐号充值清零, 删除你的订单, 删除你的评论,帖子等等, 而在比特币世界里, 矿工只做三件事情: 1.验证交易 2.记录交易 3.读交易, 矿工无法替你创建任何交易, 也无法修改你的任何交易.
在传统的中心化应用里, 中心制定规则,中心想要什么样的规则就可以有什么样的规则, 而在比特币的世界里, 规则塑造本尊,改变规则预示着分裂.
在传统的中心化应用里, 中心总是试图了解你,变得很懂你,知道你想做什么, 而在比特币世界里, 矿工只做三件事情: 1.验证交易 2.记录交易 3.读交易, 矿工不关心你是谁,也不关心你想做什么.
在传统的中心化应用里,中心经常背锅,发生了错误和损失,你第一时间想到的是向中心追责, 而在比特币世界里, 矿工只做三件事情: 1.验证交易 2.记录交易 3.读交易, 所有的错误你都得自己负责.
在某种传统的中心化应用里, 比如某个电商网站,你在上面购买了一盒牙刷, 为了购买这盒牙刷,网站中心会为你完成一系列的业务操作, 生成一系列的业务数据比如订单,支付,物流,积分等, 和网站中心相比,你实际上什么都没有干, 当然你其实点击了很多次鼠标, 打了很多字,读了很多商品评价。
但是在比特币世界里,你给某个地址转账,和矿工相比, 转账这件事情其实百分之百是你自己完成的, 交易是你创建的,矿工做的事情只不过是验证下交易,然后将交易写到区块中.
现在我们将上面的矿工都改成中心,其他不变:
传统中心和区块链的中心
在传统的中心化应用里, 中心需要做很多繁杂的事情, 而在比特币世界里, 中心只做三件事情: 1.验证交易 2.记录交易 3.读交易, 当然为了做成这三件事情,中心需要做很多其他幕后的工作。
在传统的中心化应用里, 中心接收你的命令,为你完成相关的任务, 而在比特币世界里, 中心只做三件事情: 1.验证交易 2.记录交易 3.读交易, 中心不会接受你的任何命令。
在传统的中心化应用里, 中心即使没有你的命令,也可以为你完成意想不到的任务,比如将你的帐号充值清零, 删除你的订单, 删除你的评论,帖子等等, 而在比特币世界里, 中心只做三件事情: 1.验证交易 2.记录交易 3.读交易, 中心无法替你创建任何交易, 也无法修改你的任何交易.
在传统的中心化应用里, 中心制定规则,中心想要什么样的规则就可以有什么样的规则, 而在比特币的世界里, 规则塑造本尊,改变规则预示着分裂.
在传统的中心化应用里, 中心总是试图了解你,变得很懂你,知道你想做什么, 而在比特币世界里, 中心只做三件事情: 1.验证交易 2.记录交易 3.读交易, 中心不关心你是谁,也不关心你想做什么.
在传统的中心化应用里,中心经常背锅,发生了错误和损失,你第一时间想到的是向中心追责, 而在比特币世界里, 中心只做三件事情: 1.验证交易 2.记录交易 3.读交易, 所有的错误你都得自己负责.
在某种传统的中心化应用里, 比如某个电商网站,你在上面购买了一盒牙刷, 为了购买这盒牙刷,网站中心会为你完成一系列的业务操作, 生成一系列的业务数据比如订单,支付,物流,积分等, 和网站中心相比,你实际上什么都没有干, 当然你其实点击了很多次鼠标, 打了很多字,读了很多商品评价。
但是在比特币世界里,你给某个地址转账,和中心相比, 转账这件事情其实百分之百是你自己完成的, 交易是你创建的,中心做的事情只不过是验证下交易,然后将交易写到区块中.
所以我们可以认为区块链技术是: 该由用户做的事情,只能由用户自己去做, 我们只能按规则验证用户所做的事情, 并将用户自己所做的事情如实地记录在一条链上,这条链就是区块链。
在开发区块链系统时,我们可以首先采用传统的 Client-Server 模型来进行开发设计方面的工作, 这时候我们务必保持 Server 只做 1.验证交易 2.记录交易 3.读交易 这3件事情, 然后再将 Client-Server 逐步扩展为 P2P 网络.
1. 解析交易
创世区块即比特币的第一个区块,这个区块只包含了一笔交易我们把此交易叫做创世交易, 并将它记作 Tx0,为了构造创世区块,我们首先要构造 Tx0, 为了构造 Tx0 我们需要理解比特币中的交易的数据结构.
general format of a Bitcoin transaction (inside a block)
| Field | Description | Size |
|---|---|---|
| Version no | currently 1 | 4 bytes |
| In-counter | positive integer VI = VarInt | 1 - 9 bytes |
| list of inputs | the first input of the first transaction is also called “coinbase” (its content was ignored in earlier versions) | <in-counter>-many inputs |
| Out-counter | positive integer VI = VarInt | 1 - 9 bytes |
| list of outputs | the outputs of the first transaction spend the mined bitcoins for the block | <out-counter>-many outputs |
| lock_time | if non-zero and sequence numbers are < 0xFFFFFFFF: block height or timestamp when transaction is final | 4 bytes |
为了确认自己理解了比特币交易的数据结构,最好的方式是自己写一个 parser, 然后使用自己写的这个 parser 去解析比特币交易数据的内容。我们可以使用任何自己熟悉的编程语言去写这个 parser, 但是在这篇文章中我会大部分使用 c 语言, 包括用 c 去写这个 parser, 因为我认为使用 c 语言研究区块链技术会比较直接和方便。
下面的实验中用到的文件 tx0.bin 可以从 https://github.com/baya/block7days/blob/master/tx0.bin 下载或者通过 webbtc 下载
1.1 解析 Version no
/* parse_tx_version.c */
#include <stdio.h>
int main()
{
FILE *fp;
unsigned int tx_version;
fp = fopen("tx0.bin", "rb");
fread(&tx_version, sizeof(tx_version), 1, fp);
printf("Tx Version: %u\n", tx_version);
}
通过分析 parse_tx_version.c 的代码我们可以看到用 c 语言解析比特币交易的数据结构非常直接: 定义一个 unsigned int 类型的 tx_version 变量, tx_version也是 4 bytes, 然后从 tx0.bin 的开始位置读 1 次, 读取的字节大小是 4 个字节, 这个 4 由 sizeof(tx_version) 计算出来, 读取的结果存放到 tx_version 变量里,编译上述代码,并执行,我们得到下面的输出:
Tx Version: 1
1.2 解析 In-counter
参考: https://en.bitcoin.it/wiki/Protocol_documentation#Variable_length_integer
In-counter 的结构定义如下:
Variable length integer
| Value | Storage length | Format |
|---|---|---|
| < 0xFD | 1 | uint8_t |
| <= 0xFFFF | 3 | 0xFD followed by the length as uint16_t |
| <= 0xFFFF FFFF | 5 | 0xFE followed by the length as uint32_t |
| - | 9 | 0xFF followed by the length as uint64_t |
解析的步骤如下:
-
读取第 1 个字节, 假设它的值为
v1 -
如果
v1 < 0xF, 那么 v1 就是 In-counter 的值 -
如果
v1 == 0xFD, 那么再读取 2 个字节, 这 2 个字节以 little-endian 形式存储了 In-counter 值 -
如果
v1 == 0xFE, 那么再读取 4 个字节, 这 4 个字节以 little-endian 形式存储了 In-counter 值 -
如果
v1 == 0xFF, 那么再读取 8 个字节, 这 8 个字节以 little-endian 形式存储了 In-counter 值
解析的程序分为两部分: 主程序 parse_tx_vinc.c 和用于处理 endian 的程序 kyk_endian.h, 其中 kyk_endian.h 的代码来自于 https://github.com/keeshux/basic-blockchain-programming/blob/master/endian.h
/* parse_tx_vinc.c */
#include <stdio.h>
#include <stdint.h>
int main()
{
FILE *fp;
unsigned int tx_version;
uint8_t tx_vin1;
uint16_t tx_vin2;
uint32_t tx_vin4;
uint64_t tx_vin8;
uint64_t tx_vin;
fp = fopen("tx0.bin", "rb");
fread(&tx_version, sizeof(tx_version), 1, fp);
fread(&tx_vin1, sizeof(tx_vin1), 1, fp);
if(tx_vin1 < 0xFD){
tx_vin = tx_vin1;
} else if(tx_vin1 == 0xFD){
fread(&tx_vin2, sizeof(tx_vin2), 1, fp);
tx_vin = bbp_eint16(BBP_LITTLE, tx_vin2); /* 处理 little-endian 形式的 uint16_t */
} else if(tx_vin1 == 0xFE) {
fread(&tx_vin4, sizeof(tx_vin4), 1, fp);
tx_vin = bbp_eint32(BBP_LITTLE, tx_vin4); /* 处理 little-endian 形式的 uint32_t */
} else if(tx_vin1 == 0xFF) {
fread(&tx_vin8, sizeof(tx_vin8), 1, fp);
tx_vin = bbp_eint64(BBP_LITTLE, tx_vin8); /* 处理 little-endian 形式的 uint64_t */
} else {
tx_vin = 0;
}
printf("Tx Version: %u\n", tx_version);
printf("Tx In-counter: %lld\n", tx_vin);
}
执行程序:
$ make parse_tx_vinc
$ ./parse_tx_vinc.out
Tx Version: 1
Tx In-counter: 1
1.3 解析 list of inputs
list of inputs 是由一组 Txin 构成的, Txin 的结构如下:
general format (inside a block) of each input of a transaction - Txin
| Field | Description | Size |
|---|---|---|
| Previous Transaction hash | doubled SHA256-hashed of a (previous) to-be-used transaction | 32 bytes |
| Previous Txout-index | non negative integer indexing an output of the to-be-used transaction | 4 bytes |
| Txin-script length | non negative integer VI = VarInt | 1 - 9 bytes |
| Txin-script / scriptSig | Script | <in-script length>-many bytes |
| sequence_no | normally 0xFFFFFFFF; irrelevant unless transaction’s lock_time is > 0 | 4 bytes |
为简单起见,我们只解析第一个 Txin, 我们以解析 Previous Transaction hash 为例子来讲讲解析过程。
-
Previous Transaction hash 一共有 32 个字节,为此我们定义一个长度为 32,类型为
uint8_t的数组来存储 Hash, 这个数组定义为uint8_t pre_tx_hash[32]; -
将 Hash 以 16 进制的形式存储到一个字符串中, 这个字符串定义为
char pre_tx_hash_str[65]
详细代码可以通过 https://github.com/baya/block7days/blob/master/parse_txin.c 查看.
因为 Tx0 的 Previous Transaction hash 是 “0000000000000000000000000000000000000000000000000000000000000000”, 有一定的特殊性,为了 确认解析结果是否正确,我们可以解析其他一些不特殊的交易数据,比如 https://webbtc.com/tx/703fc5…, 编译代码后我们可以给程序提供一个待解析的交易文件名为参数,比如:
$ ./a.out tx0.bin
$ ./a.out tx0.bin
Tx Version: 1
Tx In-counter: 1
Txin Previous Tx Hash: 0000000000000000000000000000000000000000000000000000000000000000
Txin Previous Txout-index: ffffffff
Txin-script length: 77
Txin-script / scriptSig: 04ffff001d0104455468652054696d65732030332f4a616e2f32303039204368616e63656c6c6f72206f6e206272696e6b206f66207365636f6e64206261696c6f757420666f722062616e6b73
Txin sequence_no: ffffffff
或者
$ ./a.out tx_703fc5ee.bin
$ ./a.out tx_703fc5ee.bin
Tx Version: 1
Tx In-counter: 1
Txin Previous Tx Hash: a59238577c596d2caa367c0855a76a75efcde6953186507fa51ee2dff3eb8b41
Txin Previous Txout-index: 1
Txin-script length: 106
Txin-script / scriptSig: 47304402207b9e4d1c1e126f47db3d74f981b8ee9c124f44a92637a657dc94cd4b05216a9a022014fe5df34c6e2c3b1bb1de3f69097873e220b97c0beefd29cc714abeb8180c880121030e1e08f6d4ba2b71207c961109f9d0b7eaad24b106ecc9b691c297c732d47fcc
Txin sequence_no: ffffffff
我们会发现解析 tx_703fc5ee.bin 的结果中 scriptSig 和 https://webbtc.com/tx/703fc5ee.json 中的 scriptSig 有些不一样, 一眼可以看出我们自己解析出的 scriptSig 前面多了 47, 这是什么原因导致的呢?回头再看 Txin 的结构表, Txin-script / scriptSig 的描述是一个 Script(https://en.bitcoin.it/wiki/Script), 比特币的 Script 是一个类似 Forth 语言的东西,我们自己写的解析器已经可以将 Script 的内容原原本本地读出来了,但是还需要将它翻译下。在后面的解析中我们会知道 47 准确地说是 0x47 其实是一个 Script Constant[28], Script Constant 是 Script OP_CODE 中的一种.
703fc5ee.json 中的 txin 的 scriptSig 的内容如下:
scriptSig: "304402207b9e4d1c1e126f47db3d74f981b8ee9c124f44a92637a657dc94cd4b05216a9a022014fe5df34c6e2c3b1bb1de3f69097873e220b97c0beefd29cc714abeb8180c8801 030e1e08f6d4ba2b71207c961109f9d0b7eaad24b106ecc9b691c297c732d47fcc"
我们自己写的解析器解析 tx_703fc5ee.bin 得到的 scriptSig 的内容如下:
scriptSig: "47304402207b9e4d1c1e126f47db3d74f981b8ee9c124f44a92637a657dc94cd4b05216a9a022014fe5df34c6e2c3b1bb1de3f69097873e220b97c0beefd29cc714abeb8180c880121030e1e08f6d4ba2b71207c961109f9d0b7eaad24b106ecc9b691c297c732d47fcc"
到目前为止, 我们的主要目的是解析 Tx0 的数据结构, 同时我们又通过解析文件 tx_703fc5ee.bin 来做一个参考检验, 我们会先把主要的精力放在解析 tx0.bin 和 tx_703fc5ee.bin 上面,所以在这篇文章中,我们后续的解析工作会继续围绕在 tx0.bin 和 tx_703fc5ee.bin 这两个文件上面, 代码的编写也会主要针对这两个文件。
1.4 解析 Txin-script / scriptSig
在这一节中我们将主要讨论解析 tx_703fc5ee.bin 和 tx0.bin 这两个文件的 Txin-script / scriptSig, 其中 tx0.bin 的 Txin-script / scriptSig 的更准确的名字应该是 coinbase scriptSig, 即属于 coinbase 交易的 scriptSig, coinbase 交易的 scriptSig 没有解锁交易的作用(因为 coinbase 交易没有输入来源不需要解锁),我们暂且简单地认为 coinbase 交易的 scriptSig 只是起到了一个占位的作用. coinbase 交易简单的理解就是创币交易,这种交易没有输入来源,用于生成比特币,它伴随着区块的产生而产生,每个区块的第一笔交易必须是 coinbase 交易,并且每个区块只能包含一笔 coinbase 交易.
scriptSig 的结构是: <Signature> <PubKey>, 也就是说 scriptSig 分为两部分:第 1 部分是 Signature, 第 2 部分是 PubKey, 那么我们如何将文件 tx_703fc5ee.bin 的 scriptSig 解析成 Signature 和 PubKey 两部分呢?
首先我们看一个表:
When talking about scripts, these value-pushing words are usually omitted.
| Word | Opcode | Hex | Input | Output | Description |
|---|---|---|---|---|---|
| OP_0, OP_FALSE | 0 | 0x00 | Nothing. | (empty value) | An empty array of bytes is pushed onto the stack. (This is not a no-op: an item is added to the stack.) |
| N/A | 1-75 | 0x01-0x4b | (special) | data | The next opcode bytes is data to be pushed onto the stack |
| OP_PUSHDATA1 | 76 | 0x4c | (special) | data | The next byte contains the number of bytes to be pushed onto the stack. |
| OP_PUSHDATA2 | 77 | 0x4d | (special) | data | The next two bytes contain the number of bytes to be pushed onto the stack. |
| OP_PUSHDATA4 | 78 | 0x4e | (special) | data | The next four bytes contain the number of bytes to be pushed onto the stack. |
| OP_1NEGATE | 79 | 0x4f | Nothing. | -1 | The number -1 is pushed onto the stack. |
| OP_1, OP_TRUE | 81 | 0x51 | Nothing. | 1 | The number 1 is pushed onto the stack. |
| OP_2-OP_16 | 82-96 | 0x52-0x60 | Nothing. | 2-16 The number in the word name (2-16) is pushed onto the stack. |
为简单起见,我们先只分析 Opcode 为 1-75 的情况, 当 1 <= Opcode <= 75 时, Opcode 后面的 Opcode 个字节的数据将被压入到栈中,这个会被压入到栈中的数据就是 Signature 或者 PubKey, 这里的栈是比特币脚本系统的一种数据结构,用于运行 Script.
通过下面的图我们可以更加直观地理解 scriptSig.

通过上图我们已经可以手工地解析出 Signature 和 PubKey, 接下来我们通过编写代码来实现解析。
详细代码可以通过链接: https://github.com/baya/block7days/blob/master/parse_txin_script_sig.c 查看.
编译文件 parse_txin_script_sig.c, 然后分别使用 tx0.bin 和 tx_703fc5ee.bin 作为输入文件进行测试,测试结果如下:
$ ./a.out tx0.bin
Tx Version: 1
Tx In-counter: 1
Txin Previous Tx Hash: 0000000000000000000000000000000000000000000000000000000000000000
Txin Previous Txout-index: ffffffff
Txin-script length: 77
Txin-script / coinbase: 04ffff001d0104455468652054696d65732030332f4a616e2f32303039204368616e63656c6c6f72206f6e206272696e6b206f66207365636f6e64206261696c6f757420666f722062616e6b73
Txin sequence_no: ffffffff
$ ./a.out tx_703fc5ee.bin
Tx Version: 1
Tx In-counter: 1
Txin Previous Tx Hash: a59238577c596d2caa367c0855a76a75efcde6953186507fa51ee2dff3eb8b41
Txin Previous Txout-index: 1
Txin-script length: 106
Txin-script / scriptSig: 304402207b9e4d1c1e126f47db3d74f981b8ee9c124f44a92637a657dc94cd4b05216a9a022014fe5df34c6e2c3b1bb1de3f69097873e220b97c0beefd29cc714abeb8180c8801 030e1e08f6d4ba2b71207c961109f9d0b7eaad24b106ecc9b691c297c732d47fcc
Txin sequence_no: ffffffff
将上面的测试结果分别与 webbtc.com 上的 TX-0 和 TX-703fc5ee 作比较,我们会发现结果是吻合的。
解析的过程是这样的,首先定义了一系列的宏, 我们只叙述用到的宏:
#define COINBASE_INX 0xffffffff
#define NULL_HASH "0000000000000000000000000000000000000000000000000000000000000000"
#define OP_PUSHDATA0_START 0x01
#define OP_PUSHDATA0_END 0x4b
#define SIG_BUF_SIZE 1000
COINBASE_INX 和 NULL_HASH 结合起来使用,用于判断 Txin(交易输入) 是否是 coinbase 类型的输入, 什么是 coinbase 呢? 简单地说就是比特币系统给你输入了一笔钱,这笔钱不是来自任何的个人。如果一个 Txin 的 Previous Txout-index 等于 COINBASE_INX 并且 Previous Tx Hash 等于 NULL_HASH, 那么这个 Txin 就是 coinbase 类型的输入.
OP_PUSHDATA0_START 和 OP_PUSHDATA0_END 结合起来使用,用于解析下面的规则:
| Word | Opcode | Hex | Input | Output | Description |
|---|---|---|---|---|---|
| N/A | 1-75 | 0x01-0x4b | (special) | data | The next opcode bytes is data to be pushed onto the stack |
对于一个非 coinbase 类型的 Txin, 当读取它的 scriptSig 时, 如果 opcode 的值是在 OP_PUSHDATA0_START 和 OP_PUSHDATA0_END 之间就需要使用上述的规则解析 scriptSig.
SIG_BUF_SIZE 用于给 coinbase 和 scriptSig 固定分配一段足够大的内存,因为 coinbase 和 scriptSig 是变长的,如果在程序运行时动态分配内存会是一件比较复杂的事情,所以我们预先设定 SIG_BUF_SIZE 为 1000 个字节,足够容纳 coinbase 或者 scriptSig.
然后我们定义 coinbase 和 scriptSig 的数据结构:
typedef struct coinbase_sig {
char sig[SIG_BUF_SIZE];
uint64_t len;
} coinbase_sig;
typedef struct script_sig {
char sig[SIG_BUF_SIZE];
char pubkey[SIG_BUF_SIZE];
uint64_t len;
} script_sig;
我们用 struct coinbase_sig 来存储 coinbase, 用 struct script_sig 来存储 scriptSig.
接着定义用于解析 coinbase 和 scriptSig 的函数:
void btc_cb_sig(coinbase_sig *sig_ptr, FILE *fp)
{
uint64_t len = sig_ptr -> len;
uint8_t sig_buf[len];
char buf3[3];
fread(sig_buf, sizeof(uint8_t), len, fp);
for(uint64_t i=0; i < len; i++)
{
get_hex2_str(buf3, sig_buf[i]);
sig_ptr->sig[i * 2] = buf3[0];
sig_ptr->sig[i * 2 + 1] = buf3[1];
}
sig_ptr->sig[len * 2] = '\0';
}
void btc_sc_sig(script_sig *sig_ptr, FILE *fp)
{
uint8_t op_code;
char buf3[3];
fread(&op_code, sizeof(uint8_t), 1, fp);
if(op_code >= OP_PUSHDATA0_START && op_code <= OP_PUSHDATA0_END){
read_op_pushdata0(sig_ptr -> sig, op_code, fp);
} else {
}
fread(&op_code, sizeof(uint8_t), 1, fp);
if(op_code >= OP_PUSHDATA0_START && op_code <= OP_PUSHDATA0_END){
read_op_pushdata0(sig_ptr -> pubkey, op_code, fp);
} else {
}
}
其中 void btc_cb_sig(coinbase_sig *sig_ptr, FILE *fp) 用于解析 coinbase, void btc_sc_sig(script_sig *sig_ptr, FILE *fp) 用于解析 scriptSig.
最后实际的解析过程如下, 去掉了一些不相关的代码,
uint32_t pre_txout_inx;
char pre_tx_hash_str[65];
uint64_t txin_script_len;
script_sig sc_sig;
coinbase_sig cb_sig;
sc_sig.len = 0;
cb_sig.len = 0;
fp = fopen(argv[1], "rb");
btc_hash(pre_tx_hash_str, fp);
pre_txout_inx = btc_uint4(fp);
txin_script_len = btc_varint(fp);
if(pre_txout_inx == COINBASE_INX && strcmp(pre_tx_hash_str, NULL_HASH) == 0){
cb_sig.len = txin_script_len;
btc_cb_sig(&cb_sig, fp);
} else {
sc_sig.len = txin_script_len;
btc_sc_sig(&sc_sig, fp);
}
1.5 解析 Txout
Txout 的格式如下:
| Field | Description | Size |
|---|---|---|
| value | non negative integer giving the number of Satoshis(BTC/10^8) to be transfered | 8 bytes |
| Txout-script length | non negative integer | 1 - 9 bytes VI = VarInt |
| Txout-script / scriptPubKey | Script | <out-script length>-many bytes |
详细代码可以通过 https://github.com/baya/block7days/blob/master/parse_txout.c 查看.
解析的过程大致如下:
1. 定义 Txout 的数据结构
typedef struct tx_out {
uint64_t value;
uint64_t len;
char *sc_pbk;
} tx_out;
Txout 的 value 的 size 是 8 bytes,所以用一个 uint64_t 类型的变量存储 value。
Txout 的 script length 是一个 1-9 bytes 的 VarInt(即可变长整型), 取最大长度,我们用一个 uint64_t 类型的变量存储 script length。
使用字符指针指向我们将来要解析出的 scriptPubKey .
2. 定义用于读取 Txout 的函数
tx_out *read_tx_out_list(uint64_t count, FILE *fp)
{
tx_out *txo_list;
uint64_t tmp;
txo_list = (tx_out*) malloc(count * sizeof(tx_out));
for(uint64_t i=0; i < count; i++){
txo_list[i].value = btc_uint8(fp);
tmp = btc_varint(fp);
txo_list[i].len = tmp;
txo_list[i].sc_pbk = btc_sc_pbk(txo_list[i].len, fp);
}
return txo_list;
}
char *btc_sc_pbk(uint64_t len, FILE *fp)
{
char *sc_pbk;
uint8_t *buf;
sc_pbk = (char *) malloc((2 * len + 1) * sizeof(char));
buf = (uint8_t *) malloc(len * sizeof(uint8_t));
fread(buf, sizeof(uint8_t), len, fp);
cp_sig_hex_to_str(sc_pbk, buf, len);
return sc_pbk;
}
3. 读取和打印 Txout
txo_list = read_tx_out_list(tx_vout, fp);
for(int i=0; i < tx_vout; i++){
printf("Txout Value: %llu\n", txo_list[i].value);
printf("Txout-script length: %llu\n", txo_list[i].len);
printf("Txout-script / scriptPubkey: %s\n", txo_list[i].sc_pbk);
}
其中 tx_vout 存储的是 Txout 的 count 值.
调试结果:
$ ./a.out tx0.bin 得到输出:
Tx Version: 1
Tx In-counter: 1
Txin Previous Tx Hash: 0000000000000000000000000000000000000000000000000000000000000000
Txin Previous Txout-index: ffffffff
Txin-script length: 77
Txin-script / coinbase: 04ffff001d0104455468652054696d65732030332f4a616e2f32303039204368616e63656c6c6f72206f6e206272696e6b206f66207365636f6e64206261696c6f757420666f722062616e6b73
Txin sequence_no: ffffffff
Txout Out-counter: 1
Txout Value: 5000000000
Txout-script length: 67
Txout-script / scriptPubkey: 4104678afdb0fe5548271967f1a67130b7105cd6a828e03909a67962e0ea1f61deb649f6bc3f4cef38c4f35504e51ec112de5c384df7ba0b8d578a4c702b6bf11d5fac
$ ./a.out tx_703fc5ee.bin 得到输出:
Tx Version: 1
Tx In-counter: 1
Txin Previous Tx Hash: a59238577c596d2caa367c0855a76a75efcde6953186507fa51ee2dff3eb8b41
Txin Previous Txout-index: 1
Txin-script length: 106
Txin-script / scriptSig: 304402207b9e4d1c1e126f47db3d74f981b8ee9c124f44a92637a657dc94cd4b05216a9a022014fe5df34c6e2c3b1bb1de3f69097873e220b97c0beefd29cc714abeb8180c8801 030e1e08f6d4ba2b71207c961109f9d0b7eaad24b106ecc9b691c297c732d47fcc
Txin sequence_no: ffffffff
Txout Out-counter: 2
Txout Value: 10000000000
Txout-script length: 25
Txout-script / scriptPubkey: 76a914a31e71f2cfc0327c55cc4026073f06f3e9e1a21a88ac
Txout Value: 10000000000
Txout-script length: 25
Txout-script / scriptPubkey: 76a914d6bbf4f08d2df7ea32b2930ae4b7436d4ca6fe4b88ac
Txout Value 以 Satoshis(BTC/10^8) 为单位.
现在读取出的 scriptPubkey 是原始的值,在 1.6 节中将解析 scriptPubkey.
1.6 解析 Txout-script / scriptPubKey
以 tx_703fc5ee.bin 中的 scriptPubkey 为例子,我们首先人肉翻译 scriptPubKey, 翻译过程如下图所示:
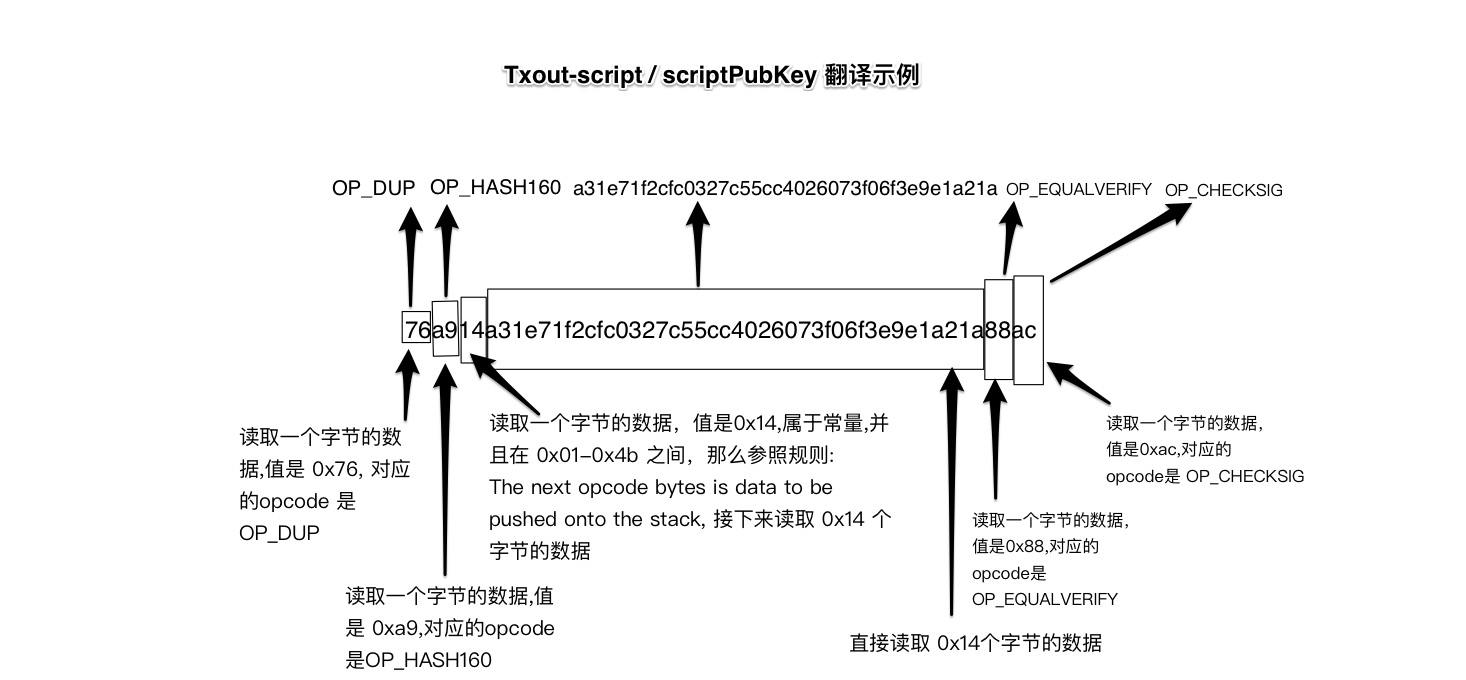
详细代码可以通过 https://github.com/baya/block7days/blob/master/parse_txout_script_pbk.c 查看.
解析的过程大致如下:
1. 定义和 opcode 相关的宏,可以在文件 parse_txout_script_pbk.c 中查看所有已经定义好的 opcode 宏
2. 定义 scriptPubkey 的数据结构, 并且将 scriptPubkey 与 Txout 关联
#define PBK_STACK_SIZE 50
typedef struct script_pbk {
char *stack[PBK_STACK_SIZE];
} script_pbk;
typedef struct tx_out {
uint64_t value;
uint64_t len;
char *sc_pbk;
script_pbk *parsed_sc_pbk;
} tx_out;
我们通过 script_pbk *parsed_sc_pbk; 将 scriptPubkey 和 Txout 关联起来
3. 定义用于把 opcode 转换为 opcode name 的索引变量.
static char *btc_sc_opcode_names[] = {"OP_FALSE","OP_PUSHDATA0_START","OP_PUSHDATA0_END","OP_PUSHDATA1","OP_PUSHDATA2","OP_PUSHDATA4","OP_1NEGATE",
"OP_TRUE","OP_2","OP_3","OP_4","OP_5","OP_6","OP_7","OP_8","OP_9","OP_10","OP_11","OP_12","OP_13","OP_14","OP_15",
"OP_16","OP_NOP","OP_IF","OP_NOTIF","OP_ELSE","OP_ENDIF","OP_VERIFY","OP_RETURN","OP_TOALTSTACK","OP_FROMALTSTACK",
"OP_IFDUP","OP_DEPTH","OP_DROP","OP_DUP","OP_NIP","OP_OVER","OP_PICK","OP_ROLL","OP_ROT","OP_SWAP","OP_TUCK","OP_2DROP",
"OP_2DUP","OP_3DUP","OP_2OVER","OP_2ROT","OP_2SWAP","OP_CAT","OP_SUBSTR","OP_LEFT","OP_RIGHT","OP_SIZE","OP_INVERT",
"OP_AND","OP_OR","OP_XOR","OP_EQUAL","OP_EQUALVERIFY","OP_1ADD","OP_1SUB","OP_2MUL","OP_2DIV","OP_NEGATE","OP_ABS",
"OP_NOT","OP_0NOTEQUAL","OP_ADD","OP_SUB","OP_MUL","OP_DIV","OP_MOD","OP_LSHIFT","OP_RSHIFT","OP_BOOLAND","OP_BOOLOR",
"OP_NUMEQUAL","OP_NUMEQUALVERIFY","OP_NUMNOTEQUAL","OP_LESSTHAN","OP_GREATERTHAN","OP_LESSTHANOREQUAL","OP_GREATERTHANOREQUAL",
"OP_MIN","OP_MAX","OP_WITHIN","OP_RIPEMD160","OP_SHA1","OP_SHA256","OP_HASH160","OP_HASH256","OP_CODESEPARATOR","OP_CHECKSIG",
"OP_CHECKSIGVERIFY","OP_CHECKMULTISIG","OP_CHECKMULTISIGVERIFY","OP_CHECKLOCKTIMEVERIFY","OP_CHECKSEQUENCEVERIFY","OP_PUBKEYHASH",
"OP_PUBKEY","OP_INVALIDOPCODE","OP_RESERVED","OP_VER","OP_VERIF","OP_VERNOTIF","OP_RESERVED1","OP_RESERVED2","OP_NOP1","OP_NOP9"};
/* generated by parse_script_optcode_to_c_array.rb */
static uint8_t btc_sc_opcodes[] = {0x00,0x01,0x4b,0x4c,0x4d,0x4e,0x4f,0x51,0x52,0x53,0x54,0x55,0x56,0x57,0x58,0x59,0x5a,0x5b,0x5c,0x5d,0x5e,0x5f,
0x60,0x61,0x63,0x64,0x67,0x68,0x69,0x6a,0x6b,0x6c,0x73,0x74,0x75,0x76,0x77,0x78,0x79,0x7a,0x7b,0x7c,0x7d,0x6d,
0x6e,0x6f,0x70,0x71,0x72,0x7e,0x7f,0x80,0x81,0x82,0x83,0x84,0x85,0x86,0x87,0x88,0x8b,0x8c,0x8d,0x8e,0x8f,0x90,
0x91,0x92,0x93,0x94,0x95,0x96,0x97,0x98,0x99,0x9a,0x9b,0x9c,0x9d,0x9e,0x9f,0xa0,0xa1,0xa2,0xa3,0xa4,0xa5,0xa6,
0xa7,0xa8,0xa9,0xaa,0xab,0xac,0xad,0xae,0xaf,0xb1,0xb2,0xfd,0xfe,0xff,0x50,0x62,0x65,0x66,0x89,0x8a,0xb0,0xb9};
4. 实现解析 scriptPubkey 的函数
script_pbk *btc_parsed_sc_pbk(uint64_t len, FILE *fp)
{
script_pbk *sc_pbk_ptr = malloc(sizeof(script_pbk));
char **stack_ptr;
uint64_t i = 0;
uint8_t opcode;
stack_ptr = sc_pbk_ptr -> stack;
do {
opcode = btc_uint1(fp);
i += 1;
if(is_sc_na_constant(opcode)){
*stack_ptr = (char *)malloc((2 * opcode + 1) * sizeof(char));
read_op_pushdata0(*stack_ptr, opcode, fp);
i += opcode;
} else {
*stack_ptr = tr_opcode_to_name(opcode);
}
++stack_ptr;
} while(i < len);
return sc_pbk_ptr;
}
void print_parsed_sc_pbk(script_pbk *sc_pbk)
{
char **stack_ptr = sc_pbk -> stack;
printf("Txout-script / Parsed scriptPubkey: ");
do{
printf("%s ", *stack_ptr);
stack_ptr++;
} while(*stack_ptr);
printf("\n");
}
int is_sc_na_constant(uint8_t opcode)
{
if(opcode >= OP_PUSHDATA0_START && opcode <= OP_PUSHDATA0_END){
return 1;
} else {
return 0;
}
}
char *tr_opcode_to_name(uint8_t opcode)
{
int i;
char *res;
size_t n = sizeof(btc_sc_opcodes) / sizeof(btc_sc_opcodes[0]);
for(i = 0; i < n; i++)
{
if(btc_sc_opcodes[i] == opcode){
break;
}
}
if(i < n){
res = btc_sc_opcode_names[i];
} else {
res = NO_FOUND_OPTCODE;
}
return res;
}
我们将解析出来的 scriptPubkey 存储到 parsed_sc_pbk 中,
txo_list[i].parsed_sc_pbk = btc_parsed_sc_pbk(txo_list[i].len, fp);
parsed_sc_pbk 其实是一个指针变量,我们用它指向 scriptPubkey 所存储的地址.
调试的结果如下:
$ ./a.out tx0.bin
Tx Version: 1
Tx In-counter: 1
Txin Previous Tx Hash: 0000000000000000000000000000000000000000000000000000000000000000
Txin Previous Txout-index: ffffffff
Txin-script length: 77
Txin-script / coinbase: 04ffff001d0104455468652054696d65732030332f4a616e2f32303039204368616e63656c6c6f72206f6e206272696e6b206f66207365636f6e64206261696c6f757420666f722062616e6b73
Txin sequence_no: ffffffff
Txout Out-counter: 1
Txout Value: 5000000000
Txout-script length: 67
Txout-script / scriptPubkey: 4104678afdb0fe5548271967f1a67130b7105cd6a828e03909a67962e0ea1f61deb649f6bc3f4cef38c4f35504e51ec112de5c384df7ba0b8d578a4c702b6bf11d5fac
Txout-script / Parsed scriptPubkey: 04678afdb0fe5548271967f1a67130b7105cd6a828e03909a67962e0ea1f61deb649f6bc3f4cef38c4f35504e51ec112de5c384df7ba0b8d578a4c702b6bf11d5f OP_CHECKSIG
$ ./a.out tx_703fc5ee.bin
Tx Version: 1
Tx In-counter: 1
Txin Previous Tx Hash: a59238577c596d2caa367c0855a76a75efcde6953186507fa51ee2dff3eb8b41
Txin Previous Txout-index: 1
Txin-script length: 106
Txin-script / scriptSig: 304402207b9e4d1c1e126f47db3d74f981b8ee9c124f44a92637a657dc94cd4b05216a9a022014fe5df34c6e2c3b1bb1de3f69097873e220b97c0beefd29cc714abeb8180c8801 030e1e08f6d4ba2b71207c961109f9d0b7eaad24b106ecc9b691c297c732d47fcc
Txin sequence_no: ffffffff
Txout Out-counter: 2
Txout Value: 10000000000
Txout-script length: 25
Txout-script / scriptPubkey: 76a914a31e71f2cfc0327c55cc4026073f06f3e9e1a21a88ac
Txout-script / Parsed scriptPubkey: OP_DUP OP_HASH160 a31e71f2cfc0327c55cc4026073f06f3e9e1a21a OP_EQUALVERIFY OP_CHECKSIG
Txout Value: 10000000000
Txout-script length: 25
Txout-script / scriptPubkey: 76a914d6bbf4f08d2df7ea32b2930ae4b7436d4ca6fe4b88ac
Txout-script / Parsed scriptPubkey: OP_DUP OP_HASH160 d6bbf4f08d2df7ea32b2930ae4b7436d4ca6fe4b OP_EQUALVERIFY OP_CHECKSIG
调试的结果和在 webbtc-tx0, webbtc-tx703fc5ee 上查询的结果一致.
2. 构造创世交易
我们可以认为一笔交易由三部分构成:
1. 交易自身的数据或者叫作交易的元数据, 这些数据有: Version no, In-counter, Out-counter, lock_time 等;
2. 交易输入数据, 记作 Txin;
3. 交易输出数据, 记作 Txout;
2.1 构造比特币协议的演示程序
首先我们给出一张创世交易 TX0 的简化图,
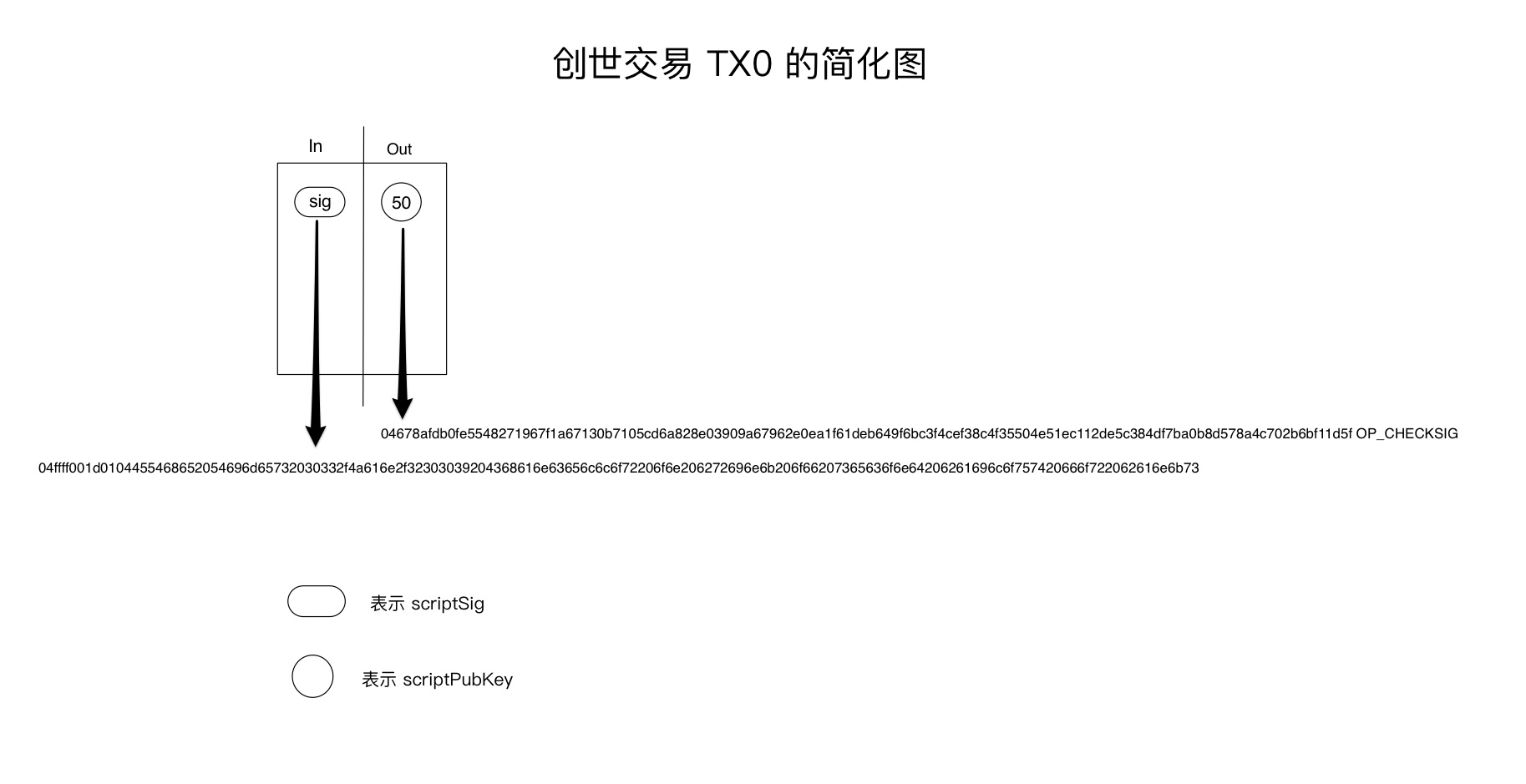
在上面的图中,我们将 TX0 的其他信息去掉了,只保留了 Txin 和 Txout 两部分的信息, 其中 In 部分包含一个 scriptSig, Out 部分包含一个 scriptPubKey.
TX0 的交易类型是: Obsolete pay-to-pubkey transaction. Obsolete 是 过时 的意思, 即 TX0 使用了 pay-to-pubkey 这种过时的交易类型,pay-to-pubkey 虽然过时了,但是比特币系统仍然会认为这种交易是合法的或者认为包含这种过时交易的历史数据是合法的。
pay-to-pubkey 这种交易的 Checking process 如下:
| Stack | Script | Description |
|---|---|---|
| Empty. | scriptSig and scriptPubKey are combined. | |
| <sig> <pubKey> | OP_CHECKSIG | Constants are added to the stack. |
| true | Empty. | Signature is checked for top two stack items. |
我们注意这句话: scriptSig and scriptPubKey are combined, 这句话的意思是将 scriptSig 和 scriptPubKey 合并起来, 如果我们刨去一些细节然后对 Checking process 进行提炼,那么 Checking process 的核心可以理解为,
将 scriptSig 和 scriptPubKey 两个脚本合并为一个脚本,然后执行合并后的脚本.
我们回到 TX0 中, TX0 中已经包含了一个 scriptSig 和一个 scriptPubKey, 那么 Checking process 是要将 TX0 中的 scriptSig 和 scriptPubKey 和并起来吗?显然不是这样的, 这里的 scriptSig 和 scriptPubKey 虽然处在同一笔交易即 TX0 中,但是两者其实是没有联系的。scriptPubKey 要合并的对象是下一笔交易的 Txin 中的 scriptSig. 在这里我们依然刨去一些细节,对创建交易这一过程进行一个抽象:
已知脚本 P, 求一脚本 S, 这个 S 满足条件: 当 S 和 P 按序合并为脚本 SP, 执行脚本 SP 后能够得到预期结果, 比如结果为 True.
现在我们根据上述抽象出来的概念来解释下为什么窃取了 private key, 就能窃取比特币。
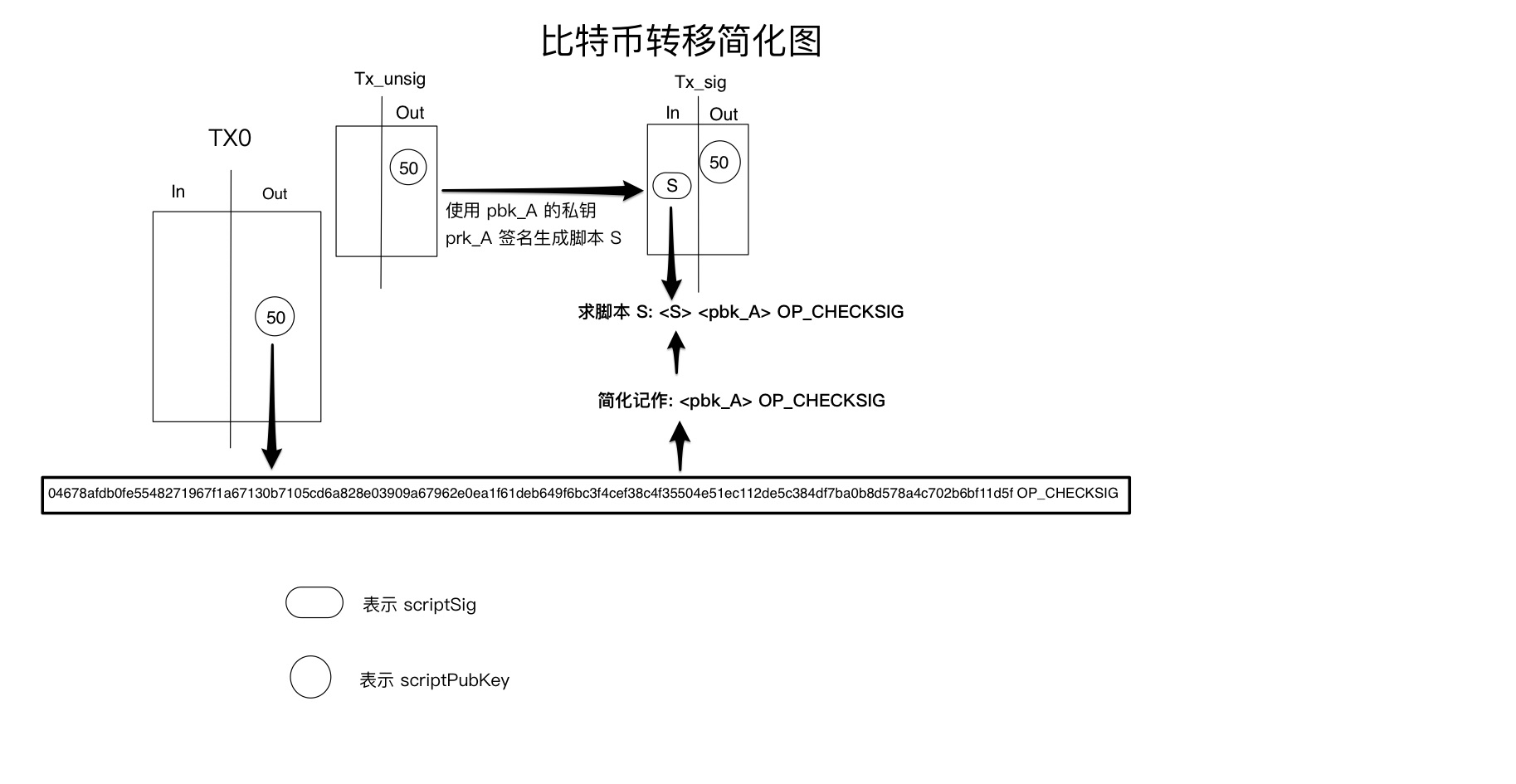
1. 首先构造一个不含 scriptSig 的交易, 记作 Tx_unsig
2. 对 Tx_unsig 作一个数字摘要,将此摘要记作 Dtxu
3. 用公钥 pbk_A 对应的私钥 prk_A 对数字摘要 Dtxu 进行一个签名得到 SigD, 这个 SigD 就是我们要求的 scriptSig: S
4. 将 S 放到 Tx_unsig 中,这时就生成了一个包含 scriptSig 的完整的交易 Tx_sig
公钥 pbk_A 能够成功验证签名S(这个逻辑是由非对称加密的原理决定的), 然后 <S> <pbk_A> OP_CHECKSIG 的求值结果为 True, 所以 Tx_sig 将是一笔合法的交易(被比特币网络承认的交易, 当然比特币网络验证一笔交易是否合法的规则还有很多,比如这笔交易的金额是否合法,是不是已经被消费过了等)。
由于我并没有中本聪的私钥,所以我没有办法用代码去演示怎么转移掉 TX0 中的 50 个比特币,但是我们可以对 Block#170 中的已经发生的交易用图形分析下如何创建可用的交易。
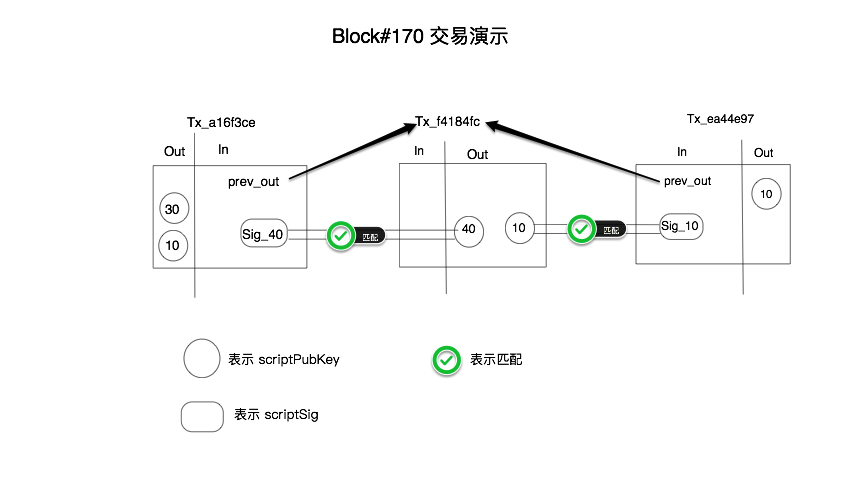
2.1.1 Message structure 即消息结构
这是一个通用的结构(Common structures), 即比特币节点之间的每一个消息的结构都是相同的, 当然消息的内容(payload)是不同的。
https://en.bitcoin.it/wiki/Protocol_documentation#Message_structure
Message structure
| Field Size | Description | Data type | Comments |
|---|---|---|---|
| 4 | magic | uint32_t | Magic value indicating message origin network, and used to seek to next message when stream state is unknown |
| 12 | command | char[12] | ASCII string identifying the packet content, NULL padded (non-NULL padding results in packet rejected) |
| 4 | length | uint32_t | Length of payload in number of bytes |
| 4 | checksum | uint32_t | First 4 bytes of sha256(sha256(payload)) |
| ? | payload | uchar[] | The actual data |
已有的 magic values:
| Network | Magic value | Sent over wire as |
|---|---|---|
| main | 0xD9B4BEF9 | F9 BE B4 D9 |
| testnet | 0xDAB5BFFA | FA BF B5 DA |
| testnet3 | 0x0709110B | 0B 11 09 07 |
| namecoin | 0xFEB4BEF9 | F9 BE B4 FE |
我们的 demo 程序将参照上面的 message structure 构造 message.
2.1.2 Message types 即消息类型
https://en.bitcoin.it/wiki/Protocol_documentation#Message_types
比特币的消息类型很多,我们暂时只分析 version, verack, tx 这3种消息,因为客户端发送一笔交易只涉及到这3种消息。
下面 3 种消息的通用结构是一致的, 不同的是 payload 结构,所以我们只分析它们的 payload 结构.
1. version
在发送交易之前,我们首先要发送 version 消息
https://en.bitcoin.it/wiki/Protocol_documentation#version
| Field Size | Description | Data type | Comments |
|---|---|---|---|
| 4 | version | int32_t | Identifies protocol version being used by the node |
| 8 | services | uint64_t | bitfield of features to be enabled for this connection |
| 8 | timestamp | int64_t | standard UNIX timestamp in seconds |
| 26 | addr_recv | net_addr | The network address of the node receiving this message |
| Fields below require version ≥ 106 | |||
| 26 | addr_from | net_addr | The network address of the node emitting this message |
| 8 | nonce | uint64_t | Node random nonce, randomly generated every time a version packet is sent. This nonce is used to detect connections to self. |
| ? | user_agent | var_str | User Agent (0x00 if string is 0 bytes long) |
| 4 | start_height | int32_t | The last block received by the emitting node |
| Fields below require version ≥ 70001 | |||
| 1 | relay | bool | Whether the remote peer should announce relayed transactions or not, see BIP 0037 |
2. verack
https://en.bitcoin.it/wiki/Protocol_documentation#verack
The verack message is sent in reply to version. This message consists of only a message header with the command string “verack”.
也就是说 verack 消息是用于反馈 version 消息的,并且只有 message header, 没有 payload, 并且它的 header 包含字符串 “verack”.
Hexdump of the verack message:
0000 F9 BE B4 D9 76 65 72 61 63 6B 00 00 00 00 00 00 ....verack......
0010 00 00 00 00 5D F6 E0 E2 ........
Message header:
F9 BE B4 D9 - Main network magic bytes
76 65 72 61 63 6B 00 00 00 00 00 00 - "verack" command
00 00 00 00 - Payload is 0 bytes long
5D F6 E0 E2 - Checksum
3. tx
这个才是我们的主角,它的 payload 结构其实就是一个交易: Tx.
https://en.bitcoin.it/wiki/Protocol_documentation#tx
我们已经在第 1 节里对 Tx 的结构做了大量的解析工作,这里就不再重复叙述 Tx 的结构了.
2.1.4 实现 version 消息
可以通过链接 https://github.com/baya/block7days/tree/master/protocols/btc_version 访问此部分相关的代码.
由于我没有其他机器,这篇文章目前所有的代码都只在 macOS-10.12.6 即 macOS Sierra 上测试过. 编译过程如下:
1. cd btc_version,执行 make btc_version
2. 执行 ./btc_version.out, 输出:
connected success: 5
Received 150 bytes: ????version
?U9???j?b??f|?ċ
I?/Satoshi:0.14.2/Q????verack]???
btc_version 会向真实的 Bitcoin 节点发送 version 消息, 我们可以看到节点向我们反馈了 /Satoshi:0.14.2/ 的信息. 下面我们介绍下 btc_version 内一些文件的作用和意义.
beej_pack.c 的主要内容来源于 http://beej.us/guide/bgnet/output/html/multipage/advanced.html#serialization. 因为 Bitcoin 协议中的很多数据是以 little-endian 形式编码的, 所以我对 beej_pack.c 进行了一些扩展,以使它支持 little-endian 形式的打包和解包,
打包就是编码数据,解包就是解码数据.
打包的格式如下:
/*
** pack() -- store data dictated by the format string in the buffer
**
** bits |byte order float alignment
** -----+------------------------------------------
** < | little-endian standard none
** > | big-endian standard none
**
** bits |signed unsigned float string
** -----+----------------------------------
** 8 | c C
** 16 | h H f
** 32 | l L d
** 64 | q Q g
** - | s
**
** (16-bit unsigned length is automatically prepended to strings)
*/
解包的格式如下:
/*
** unpack() -- unpack data dictated by the format string into the buffer
**
** bits |byte order float alignment
** -----+------------------------------------------
** < | little-endian standard none
** > | big-endian standard none
**
** bits |signed unsigned float string
** -----+----------------------------------
** 8 | c C
** 16 | h H f
** 32 | l L d
** 64 | q Q g
** - | s
**
** (string is extracted based on its stored length, but 's' can be
** prepended with a max length)
*/
kyk_sha.c 对 openssl 中的 sha256 API 进行了一些简单的封装, 其中的 kyk_dble_sha256 函数能够对数据做两次 sha256, 这样就能方便地实现 sha256(sha256(payload)),
unsigned char * kyk_dble_sha256(const char *str, size_t len)
{
unsigned char *dg1;
unsigned char *dg2;
dg1 = kyk_sha256(str, len);
dg2 = kyk_sha256((char *)dg1, SHA256_DIGEST_LENGTH);
free(dg1);
return dg2;
}
kyk_socket.c 中的 kyk_send_btc_msg_buf 函数对一些 socket API 进行了封装,实现了查找,连接 Bitcoin 服务节点的功能,并能够将打包好的数据发送给 Bitcoin 服务节点。
kyk_send_btc_msg_buf("seed.bitcoin.sipa.be", "8333", &msg_buf);
btc_message.h 主要是定义了一些和 message, version 相关的数据结构。
btc_message.c 主要定义了一个函数: ptl_msg * unpack_resp_buf(ptl_resp_buf *resp_buf), 这个函数的作用是将比特币节点响应的数据解析为可读的消息.当我们向比特币节点发送 version 消息时,我们可以使用 unpack_resp_buf 解析节点响应的数据,我们可以得到类似下面的输出:
f9beb4d9 ............................ Start String: Mainnet
76657273696f6e0000000000 ............ Command name
Command name: version
66000000 ............................ Payload size
63e84674 ............................ Checksum
7f1101000c000000000000008d01905900000000000000000000000000000000000000000000ffffaf0b6ec9fdc10c000000000000000000000000000000000000000000000000005e072a53686db942102f5361746f7368693a302e31342e322f4554070001 Payload
f9beb4d976657273696f6e00000000006600000063e846747f1101000c000000000000008d01905900000000000000000000000000000000000000000000ffffaf0b6ec9fdc10c000000000000000000000000000000000000000000000000005e072a53686db942102f5361746f7368693a302e31342e322f4554070001
7f110100 ............................ ptl_ver.vers
0c00000000000000 .................... ptl_ver.servs
8d01905900000000 .................... ptl_ver.ttamp
0000000000000000 .................... ptl_ver.addr_recv_ptr -> servs
00000000000000000000ffffaf0b6ec9 .... ptl_ver.addr_recv_ptr -> ipv
fdc1 ................................ ptl_ver.addr_recv_ptr -> port
0c00000000000000 .................... ptl_ver.addr_from_ptr -> servs
00000000000000000000000000000000 .... ptl_ver.addr_from_ptr -> ipv
0000 ................................ ptl_ver.addr_from_ptr -> port
5e072a53686db942 .................... ptl_ver.nonce
102f ................................ ptl_ver.ua_len
5361746f7368693a302e31342e322f45 .... ptl_ver.uagent
uagent: Satoshi:0.14.2/ET
54070001 ............................ ptl_ver.start_height
7d .................................. ptl_ver.relay
通过阅读上面的输出信息, 我们可以知道节点响应给我们的消息类型也是 version, 并且 uagent 是 Satoshi:0.14.2/ET, 注意这里节点响应给我们的 uagent 并不是一成不变的,不同的节点会响应给我们不同的 uagent.
76657273696f6e0000000000 ............ Command name
Command name: version
5361746f7368693a302e31342e322f45 .... ptl_ver.uagent
uagent: Satoshi:0.14.2/ET
btc_version.c 中包含了 main 函数,这个文件的主要作用是填充了 version 消息,并将消息打包,最后将打包好的消息发送给 Bitcoin 节点.
2.1.5 实现 verack 消息
可以通过链接 https://github.com/baya/block7days/tree/master/protocols/btc_verack 访问 verack 相关的代码.
verack 码和 version 的大部分代码是一样的,verack 消息由于没有 payload, 所以它的消息构造比较简单,其 main 函数所在的主文件 btc_verack.c 也比较简单.
编译 verack,
$ make btc_verack
执行 btc_verack.out,
$ ./btc_verack.out
输出:
connected success: 5
Received 0 bytes:
=======> Request Buf:
f9beb4d9 ............................ Start String: Mainnet
76657261636b000000000000 ............ Command name
Command name: verack
00000000 ............................ Payload size
5df6e0e2 ............................ Checksum
.................................... Payload
f9beb4d976657261636b000000000000000000005df6e0e2
=======> Response Buf:
00000000 ............................ Start String: Mainnet
000000000000000000000000 ............ Command name
Command name:
00000000 ............................ Payload size
00000000 ............................ Checksum
.................................... Payload
000000000000000000000000000000000000000000000000
从上面打印的信息可以看到比特币节点貌似不会对 verack 消息作出响应,其响应的字节数为 0.
从 https://en.bitcoin.it/wiki/Protocol_documentation#verack 看到一句话,
The verack message is sent in reply to version.
这句话的意思是: verack 消息是用来响应 version 消息的,按我的猜想应该是客户端在收到节点响应的 version 消息后可以向节点反馈一个 verack 消息.
2.1.6 实现 BTC Echo 服务
BTC Echo 服务是我自己要构建的一个服务,它与比特币的官方协议没有任何关系,我构建这个服务主要是为了达成以下两个目标:
1. 将客户端发过来的数据解析成对人类友好的可读格式, 以方便调试客户端发送的数据是否正确;
2. 为后面实现一个可用的比特币 demo 节点搭建一个初步的代码框架;
BTC Echo 的代码可以通过 https://github.com/baya/block7days/tree/master/protocols/btc_echo 访问.
主要的逻辑是在 btc_echo.c 这个文件中实现的, 并且 btc_echo.c 主要遵循上图所示的套路:
socket() –> bind() –> listen() –> accept() –> recv() –> send() –> close()
编译和测试步骤如下, 注意这些步骤都是在 btc_echo 目录下执行,
1. 编译 btc_echo
$ make btc_echo
2. 编译 btc_verack
$ make btc_verack
3. 启动 btc_echo 服务
$ ./btc_echo.out
4. 发起 verack 请求
$ ./btc_verack.out
可以得到如下信息:
Received 104 bytes
=======> Response Body:
Magic: f9beb4d9
Command: 76657261636b000000000000
Payload Length: 00000000
Checksum: 5df6e0e2
Payload:
BTC echo 服务已经可以将 message header 正确地解析出来,并且将解析后的结果以对人类友好的格式发送给请求端.
我们可以继续实验下 echo version 消息的效果.
1. 编译 btc_version
$ make btc_version
2. 执行 btc_version
$ ./btc_version.out
3. 请求的结果
connected success: 5
Received 276 bytes
=======> Response Body:
Magic: f9beb4d9
Command: 76657273696f6e0000000000
Payload Length: 56000000
Checksum: af577224
Payload: 7e11010001000000000000003a03955900000000010000000000000000000000000000000000ffff7f000001208d010000000000000000000000000000000000ffff7f000001208d00000000000000000000cf050500
2.2 构造我们自己的创世交易
在中本聪比特币系统中,创世交易 Tx0 是这样的:
{
hash: "4a5e1e4baab89f3a32518a88c31bc87f618f76673e2cc77ab2127b7afdeda33b",
ver: 1,
vin_sz: 1,
vout_sz: 1,
lock_time: 0,
size: 204,
in: [
{
prev_out: {
hash: "0000000000000000000000000000000000000000000000000000000000000000",
n: 4294967295
},
coinbase: "04ffff001d0104455468652054696d65732030332f4a616e2f32303039204368616e63656c6c6f72206f6e206272696e6b206f66207365636f6e64206261696c6f757420666f722062616e6b73"
}
],
out: [
{
value: "50.00000000",
scriptPubKey: "04678afdb0fe5548271967f1a67130b7105cd6a828e03909a67962e0ea1f61deb649f6bc3f4cef38c4f35504e51ec112de5c384df7ba0b8d578a4c702b6bf11d5f OP_CHECKSIG"
}
],
nid: "c2151f94f6ca6cecbe5d17cd12aaa40e5b1571ca10da82f2f5bcdb6205dcad6a",
block: "000000000019d6689c085ae165831e934ff763ae46a2a6c172b3f1b60a8ce26f",
blocknumber: 0,
time: "2009-01-03 18:15:05"
}
首先我们会构造一个和 Tx0 几乎一摸一样的创世交易, 为了和中本聪的比特币系统相区别,将我们自己构造的创世交易记作: kyk_Tx0, 然后我们会对 kyk_Tx0 进行升级,比如把 scriptPubKey 从 pay-to-pubkey 类型升级为 pay-to-pubkey-hash 类型.
关于比特币的 script 类型, 我们可以通过阅读 https://en.bitcoin.it/wiki/Script 获得更详细的细节, 其中 pay-to-pubkey 可以简单理解为向一个 pubkey 转帐, pay-to-pubkey-hash 可以简单理解为向 pubkey 的 hash 串(即比特币地址)进行转帐.
pay-to-pubkey-hash 相对于 pay-to-pubkey 的优势是 pay-to-pubkey-hash 隐藏掉了公钥, 直到你需要将你地址上的比特币发出去时,才会公开你的公钥, 更深的细节我们将在后面逐一叙述.
2.2.1 Copy Tx0 to kyk_Tx0
创世交易是如此的重要,如果创世交易包含错误,那就意味着我们自己构建的整个区块链系统都是错误的, 为了验证我们自己创建的第一笔交易是否是正确的,比较直接的方式就是以现有的比特币系统的创世交易的数据为目标生成对象, 如果我们的程序能够”山寨”一笔和中本聪比特币系统一模一样的创世交易,那么至少可以部分证明我们的程序是可靠的,验证主要分成两个部分: 1. 验证是否生成了相同的字节数据; 2. 验证是否生成了相同的 hash
首先这一部分内容的相关代码可以通过 btc_tx 访问, 可以通过运行 make kyk_tx0 生成 kyk_tx0.out 程序.
1. 验证是否生成了相同的字节数据
比特币创世交易的字节数据可以通过链接https://webbtc.com/tx/4a5e1e4baab89f3a32518a88c31bc87f618f76673e2cc77ab2127b7afdeda33b.hex 访问, 它的内容如下:
01000000010000000000000000000000000000000000000000000000000000000000000000ffffffff4d04ffff001d0104455468652054696d65732030332f4a616e2f32303039204368616e63656c6c6f72206f6e206272696e6b206f66207365636f6e64206261696c6f757420666f722062616e6b73ffffffff0100f2052a01000000434104678afdb0fe5548271967f1a67130b7105cd6a828e03909a67962e0ea1f61deb649f6bc3f4cef38c4f35504e51ec112de5c384df7ba0b8d578a4c702b6bf11d5fac00000000
执行 ./kyk_tx0.out 我们的程序会输出和上面相同的 hex 字符串.
2. 验证是否生成了相同的 hash
比特币交易的 hash 也称作交易 ID, 即 TransactionID, 简记为 Txid, 这个 Txid 是通过对上面的字节数据做两次 SHA-256 运算,并且将计算结果进行倒序操作得到的, 为什么要计算两次 SHA-256, 为什么要进行倒序操作, 我现在无从知晓其具体原因[why-double-hash]. 计算 Txid 的代码可以通过 kyk_sha.c 查看:
/* 进行两次 SHA-256 计算 */
unsigned char * kyk_dble_sha256(const char *str, size_t len)
{
unsigned char *dg1;
unsigned char *dg2;
dg1 = kyk_sha256(str, len);
dg2 = kyk_sha256((char *)dg1, SHA256_DIGEST_LENGTH);
free(dg1);
return dg2;
}
/* 使用 kyk_dble_sha256 函数进行两次 SHA-256 计算,然后将计算结果倒序 */
struct kyk_hash *kyk_inver_hash(const char *src, size_t len)
{
unsigned char *dg;
struct kyk_hash *ivhash;
size_t dg_len = SHA256_DIGEST_LENGTH;
dg = kyk_dble_sha256(src, len);
ivhash = (struct kyk_hash*) malloc(sizeof(struct kyk_hash));
ivhash -> len = dg_len;
ivhash -> body = (unsigned char*)malloc(dg_len * sizeof(unsigned char));
if(ivhash -> body == NULL){
fprintf(stderr, "failed in malloc kyk inver hash\n");
exit(1);
}
for(int i=dg_len -1; i >= 0; i--){
ivhash->body[dg_len - 1 - i] = dg[i];
}
free(dg);
return ivhash;
}
比特币创世交易的 hash 是 4a5e1e4baab89f3a32518a88c31bc87f618f76673e2cc77ab2127b7afdeda33b
执行 ./kyk_tx0.out 后,我们的程序会输出和比特币创世交易相同的 hash: 4a5e1e4baab89f3a32518a88c31bc87f618f76673e2cc77ab2127b7afdeda33b
kyk_tx0.out 的输出结果:
====>hex: 01000000010000000000000000000000000000000000000000000000000000000000000000ffffffff4d04ffff001d0104455468652054696d65732030332f4a616e2f32303039204368616e63656c6c6f72206f6e206272696e6b206f66207365636f6e64206261696c6f757420666f722062616e6b73ffffffff0100f2052a01000000434104678afdb0fe5548271967f1a67130b7105cd6a828e03909a67962e0ea1f61deb649f6bc3f4cef38c4f35504e51ec112de5c384df7ba0b8d578a4c702b6bf11d5fac00000000
====>hash: 4a5e1e4baab89f3a32518a88c31bc87f618f76673e2cc77ab2127b7afdeda33b
可以通过 kyk_tx0.c 查看用于复制比特币创世交易的主程序.
2.2.2 升级 kyk_Tx0, 构造自己掌控的创世交易
这一小节的所有代码可以通过 https://github.com/baya/block7days/tree/master/protocols/kyk_gens_tx 访问.
构造自己掌控的创世交易意味着我们需要使用自己的私钥去构造创世交易. 在这一小节我们主要需要解决下面的问题:
-
如何生成比特币地址?
-
如何生成 scriptPubKey ?
-
如何生成 scriptSig ?
-
如何执行 Pay-to-PubkeyHash 脚本 ?
2.2.2.1 生成比特币地址
对于如何生成比特地址这个问题, 链接 https://en.bitcoin.it/wiki/Technical_background_of_version_1_Bitcoin_addresses 给出了非常清晰的解决步骤.
0 - Having a private ECDSA key
18E14A7B6A307F426A94F8114701E7C8E774E7F9A47E2C2035DB29A206321725
1 - Take the corresponding public key generated with it (65 bytes, 1 byte 0x04, 32 bytes corresponding to X coordinate, 32 bytes corresponding to Y coordinate)
0450863AD64A87AE8A2FE83C1AF1A8403CB53F53E486D8511DAD8A04887E5B23522CD470243453A299FA9E77237716103ABC11A1DF38855ED6F2EE187E9C582BA6
2 - Perform SHA-256 hashing on the public key
600FFE422B4E00731A59557A5CCA46CC183944191006324A447BDB2D98D4B408
3 - Perform RIPEMD-160 hashing on the result of SHA-256
010966776006953D5567439E5E39F86A0D273BEE
4 - Add version byte in front of RIPEMD-160 hash (0x00 for Main Network)
00010966776006953D5567439E5E39F86A0D273BEE
(note that below steps are the Base58Check encoding, which has multiple library options available implementing it)
5 - Perform SHA-256 hash on the extended RIPEMD-160 result
445C7A8007A93D8733188288BB320A8FE2DEBD2AE1B47F0F50BC10BAE845C094
6 - Perform SHA-256 hash on the result of the previous SHA-256 hash
D61967F63C7DD183914A4AE452C9F6AD5D462CE3D277798075B107615C1A8A30
7 - Take the first 4 bytes of the second SHA-256 hash. This is the address checksum
D61967F6
8 - Add the 4 checksum bytes from stage 7 at the end of extended RIPEMD-160 hash from stage 4. This is the 25-byte binary Bitcoin Address.
00010966776006953D5567439E5E39F86A0D273BEED61967F6
9 - Convert the result from a byte string into a base58 string using Base58Check encoding. This is the most commonly used Bitcoin Address format
16UwLL9Risc3QfPqBUvKofHmBQ7wMtjvM
可以通过 kyk_address_test.c 访问生成比特币地址的样例代码, kyk_address_test.c 依次实现了上述的生成比特币地址的 0-9 的 10 个步骤.
#include <stdio.h>
#include <stdlib.h>
#include <unistd.h>
#include <string.h>
#include "kyk_ecdsa.h"
#include "kyk_utils.h"
#include "kyk_sha.h"
#include "kyk_base58.h"
#define MAIN_NW 0x00
void set_version_byte(uint8_t *vdgst, uint8_t *digest, uint8_t vbyt, size_t len);
void get_addr_checksum(uint8_t *dgst7, const uint8_t *dgst6, size_t len);
void set_chksum_byte(uint8_t *dgst8,
uint8_t *dgst7, size_t len1,
uint8_t *dgst4, size_t len2);
int main()
{
/*
* 0 - Having a private ECDSA key
*/
uint8_t priv_bytes[32] = {
0x18,0xE1,0x4A,0x7B,0x6A,0x30,0x7F,0x42,
0x6A,0x94,0xF8,0x11,0x47,0x01,0xE7,0xC8,
0xE7,0x74,0xE7,0xF9,0xA4,0x7E,0x2C,0x20,
0x35,0xDB,0x29,0xA2,0x06,0x32,0x17,0x25
};
EC_KEY *key;
uint8_t priv[32];
const BIGNUM *priv_bn;
point_conversion_form_t conv_form = POINT_CONVERSION_UNCOMPRESSED;
size_t pub_len;
uint8_t *pub, *pub_copy;
uint8_t *sha_pub;
uint8_t dgst3[20];
uint8_t dgst4[21];
uint8_t dgst5[32];
uint8_t dgst6[32];
uint8_t dgst7[4];
uint8_t dgst8[25];
char *dgst9;
key = kyk_ec_new_keypair(priv_bytes);
if (!key) {
fprintf(stderr, "Unable to create keypair\n");
return -1;
}
priv_bn = EC_KEY_get0_private_key(key);
if (!priv_bn) {
fprintf(stderr, "Unable to decode private key\n");
return -1;
}
BN_bn2bin(priv_bn, priv);
printf("\nHow to create Bitcoin Address?\n\n");
printf("0 - Having a private ECDSA key\n");
kyk_print_hex("", priv, sizeof(priv));
printf("\n");
BN_bn2bin(priv_bn, priv);
EC_KEY_set_conv_form(key, conv_form);
pub_len = i2o_ECPublicKey(key, NULL);
pub = calloc(pub_len, sizeof(uint8_t));
pub_copy = pub;
/*
* 1 - Take the corresponding public key generated with it
* (
* 65 bytes, 1 byte 0x04,
* 32 bytes corresponding to X coordinate,
* 32 bytes corresponding to Y coordinate
* )
*
*/
if (i2o_ECPublicKey(key, &pub_copy) != pub_len) {
fprintf(stderr, "Unable to decode public key\n");
return -1;
}
printf("1 - Take the corresponding public key generated with it (65 bytes, 1 byte 0x04, 32 bytes corresponding to X coordinate, 32 bytes corresponding to Y coordinate)\n");
kyk_print_hex("", pub, pub_len);
printf("\n");
/*
* 2 - Perform SHA-256 hashing on the public key
*/
sha_pub = kyk_sha256((char *)pub, pub_len);
printf("2 - Perform SHA-256 hashing on the public key\n");
kyk_print_hex("", sha_pub, SHA256_DIGEST_LENGTH);
printf("\n");
/*
* 3 - Perform RIPEMD-160 hashing on the result of SHA-256
*/
kyk_dgst_rmd160(dgst3, sha_pub, SHA256_DIGEST_LENGTH);
printf("3 - Perform RIPEMD-160 hashing on the result of SHA-256\n");
kyk_print_hex("", dgst3, sizeof(dgst3));
printf("\n");
/*
* 4 - Add version byte in front of RIPEMD-160 hash (0x00 for Main Network)
*/
set_version_byte(dgst4, dgst3, MAIN_NW, 20);
printf("4 - Add version byte in front of RIPEMD-160 hash (0x00 for Main Network)\n");
kyk_print_hex("", dgst4, sizeof(dgst4));
printf("\n");
/*
* 5 - Perform SHA-256 hash on the extended RIPEMD-160 result
*/
kyk_dgst_sha256(dgst5, dgst4, sizeof(dgst4));
printf("5 - Perform SHA-256 hash on the extended RIPEMD-160 result\n");
kyk_print_hex("", dgst5, sizeof(dgst5));
printf("\n");
/*
* 6 - Perform SHA-256 hash on the result of the previous SHA-256 hash
*/
kyk_dgst_sha256(dgst6, dgst5, sizeof(dgst5));
printf("6 - Perform SHA-256 hash on the result of the previous SHA-256 hash\n");
kyk_print_hex("", dgst6, sizeof(dgst6));
printf("\n");
/*
* 7 - Take the first 4 bytes of the second SHA-256 hash. This is the address checksum
*/
get_addr_checksum(dgst7, dgst6, sizeof(dgst7));
printf("7 - Take the first 4 bytes of the second SHA-256 hash. This is the address checksum\n");
kyk_print_hex("", dgst7, sizeof(dgst7));
printf("\n");
/*
* 8 - Add the 4 checksum bytes from stage 7 at the end of extended RIPEMD-160 hash from stage 4. This is the 25-byte binary Bitcoin Address.
*/
set_chksum_byte(dgst8, dgst7, sizeof(dgst7), dgst4, sizeof(dgst4));
printf("8 - Add the 4 checksum bytes from stage 7 at the end of extended RIPEMD-160 hash from stage 4. This is the 25-byte binary Bitcoin Address.\n");
kyk_print_hex("", dgst8, sizeof(dgst8));
printf("\n");
/*
* 9 - Convert the result from a byte string into a base58 string using Base58Check encoding. This is the most commonly used Bitcoin Address format
*/
dgst9 = kyk_base58(dgst8, sizeof(dgst8));
printf("9 - Convert the result from a byte string into a base58 string using Base58Check encoding. This is the most commonly used Bitcoin Address format\n");
printf("%s\n", dgst9);
EC_KEY_free(key);
free(sha_pub);
free(dgst9);
return 0;
}
void set_version_byte(uint8_t *vdgst, uint8_t *digest, uint8_t vbyt, size_t len)
{
vdgst[0] = vbyt;
for (int i=0; i < len; i++){
vdgst[i+1] = digest[i];
}
}
void get_addr_checksum(uint8_t *dgst7, const uint8_t *dgst6, size_t len)
{
for(int i=0; i < len; i++){
dgst7[i] = dgst6[i];
}
}
void set_chksum_byte(uint8_t *dgst8,
uint8_t *dgst7, size_t len1,
uint8_t *dgst4, size_t len2)
{
for(int i=0; i < len2; i++){
dgst8[i] = dgst4[i];
}
for(int j=0; j < len1; j++){
dgst8[j+len2] = dgst7[j];
}
}
编译和执行 kyk_address_test,
$ make kyk_address_test && ./kyk_address_test.out
我们会得到一个比特币地址: 16UwLL9Risc3QfPqBUvKofHmBQ7wMtjvM, 这个比特币地址和 https://en.bitcoin.it/wiki/Technical_background_of_version_1_Bitcoin_addresses 中给出的比特币地址: 16UwLL9Risc3QfPqBUvKofHmBQ7wMtjvM 是一样的, 这就确认了我们编写的用于计算比特币地址的代码是正确的. 我们可以预设置不同的 private key, 从而生成不同的比特币地址.
2.2.2.2 生成创世交易的地址
首先我们用 openssl 命令行来生成一个私钥,这个私钥将用于我们后面一系列的实践,并且我会将这个私钥公开出来.
$ openssl ecparam -name secp256k1 -genkey -out kyk-gens-priv.pem
上面的那条命令可以生成一个私钥文件: kyk-gens-priv.pem, 执行 cat kyk-gens-priv.pem 查看文件内容如下:
-----BEGIN EC PARAMETERS-----
BgUrgQQACg==
-----END EC PARAMETERS-----
-----BEGIN EC PRIVATE KEY-----
MHQCAQEEIGyF85RRQabEN5NWWhfDxGnEyweKFzUsInq7yFiVGqDyoAcGBSuBBAAK
oUQDQgAE08/t5Wp59raQel8UWnbMXNdUmyRPfZO7ctT55GGxRqkO/XIRmst49RSl
MtAXYdDLxDHYkdKdiBAREFYFMdlhJQ==
-----END EC PRIVATE KEY-----
文件里面的私钥是经过 base64 编码的,我们可以用 openssl 对其进行解码(decode),
$ openssl ec -in kyk-gens-priv.pem -text -noout
解码结果如下, 其中显示了私钥和公钥,
Private-Key: (256 bit)
priv:
6c:85:f3:94:51:41:a6:c4:37:93:56:5a:17:c3:c4:
69:c4:cb:07:8a:17:35:2c:22:7a:bb:c8:58:95:1a:
a0:f2
pub:
04:d3:cf:ed:e5:6a:79:f6:b6:90:7a:5f:14:5a:76:
cc:5c:d7:54:9b:24:4f:7d:93:bb:72:d4:f9:e4:61:
b1:46:a9:0e:fd:72:11:9a:cb:78:f5:14:a5:32:d0:
17:61:d0:cb:c4:31:d8:91:d2:9d:88:10:11:10:56:
05:31:d9:61:25
ASN1 OID: secp256k1
现在我们要写一个程序,它能够直接读取 kyk-gens-priv.pem 文件的内容,然后生成一个地址.
#include <stdio.h>
#include <stdlib.h>
#include <unistd.h>
#include <openssl/pem.h>
#include "kyk_address.h"
int main()
{
uint8_t priv[32];
EVP_PKEY *evp_key;
EC_KEY *ec_key;
const BIGNUM *priv_bn;
char *addr;
FILE *fp = fopen("kyk-gens-priv.pem", "r");
if(!fp){
perror("Pem File opening failed");
return EXIT_FAILURE;
}
/* 提取类型为 EVP_PKEY 的私钥 */
evp_key = PEM_read_PrivateKey(fp, NULL, NULL, NULL);
if (!evp_key) {
fprintf(stderr, "Unable to read pem\n");
return -1;
}
/* EVP_PKEY 转换为 EC_KEY */
ec_key = EVP_PKEY_get1_EC_KEY(evp_key);
/* EC_KEY 转换为大数 BIGNUM*/
priv_bn = EC_KEY_get0_private_key(ec_key);
/* BIGNUM 转换为私钥字节 */
BN_bn2bin(priv_bn, priv);
kyk_print_hex("private key ", priv, sizeof(priv));
/* 从私钥字节生成地址 */
addr = kyk_make_address(priv);
printf("address : %s\n", addr);
EC_KEY_free(ec_key);
EVP_PKEY_free(evp_key);
free(addr);
fclose(fp);
return 0;
}
编译执行 make pem_to_address && ./pem_to_address.out, 输出:
private key : 6c85f3945141a6c43793565a17c3c469c4cb078a17352c227abbc858951aa0f2
address : 1Te2roqFCPbG59tTP4fLjCZpEAiiwXAQm
当然我们可以对 pem_to_address.c 进行一些改进使它可以接收 pem 文件名作为参数,以生成对应的 address, 但是为了方便后面的实践和叙述我们就限定 1Te2roqFCPbG59tTP4fLjCZpEAiiwXAQm 为
创世交易的地址.
接下来我们再编写一个 python 程序,使用相同的 private key, 看是否能够生成和上面一样的 address.
这个 python 程序可以通过 btc_addr.py 访问, 需要安装 python3, 然后使用 pip3 安装 ecdsa: pip3 install ecdsa,
$ python3 btc_addr.py
1Te2roqFCPbG59tTP4fLjCZpEAiiwXAQm
输出结果也是 1Te2roqFCPbG59tTP4fLjCZpEAiiwXAQm, 这就验证了我们的 pem_to_address.c 程序的正确性.
在写作过程中我发现了另外一个查询比特币数据的 API: https://blockexplorer.com/api-ref, 后续实践我们也会以 https://blockexplorer.com/api-ref 中查询到的数据作为参考对象.
为了方便查询数据,我用 ruby 写了一个程序以方便调用 API, 可以通过 bexp.rb查看这个 ruby 程序, 使用示例:
- 查看 block
$ ./bexp.rb block/0000000000000000079c58e8b5bce4217f7515a74b170049398ed9b8428beb4a
- 验证 address
$ ./bexp.rb addr-validate/1Te2roqFCPbG59tTP4fLjCZpEAiiwXAQm
true
1Te2roqFCPbG59tTP4fLjCZpEAiiwXAQm 即我们自己构造的创世地址,它通过了验证.
2.2.2.3 生成 scriptPubKey
这个链接 https://en.bitcoin.it/wiki/Transaction#Pay-to-PubkeyHash 给出了 Pay-to-PubkeyHash script 的详细结构,其中也包含了 scriptPubKey 的结构, 对于不同的 script, 它的 scriptPubKey 也是不一样的,这里我们 只研究 Pay-to-PubkeyHash script 的 scriptPubKey.
| Stack | Script | Description |
|---|---|---|
| Empty. | <sig> <pubKey> OP_DUP OP_HASH160 <pubKeyHash> OP_EQUALVERIFY OP_CHECKSIG | scriptSig and scriptPubKey are combined. |
| <sig> <pubKey> | OP_DUP OP_HASH160 <pubKeyHash> OP_EQUALVERIFY OP_CHECKSIG | Constants are added to the stack. |
| <sig> <pubKey> <pubKey> | OP_HASH160 <pubKeyHash> OP_EQUALVERIFY OP_CHECKSIG | Top stack item is duplicated. |
| <sig> <pubKey> <pubHashA> <pubKeyHash> | OP_EQUALVERIFY OP_CHECKSIG | Top stack item is hashed. |
| <sig> <pubKey> <pubHashA> <pubKeyHash> | OP_EQUALVERIFY OP_CHECKSIG | Constant added. |
| <sig> <pubKey> | OP_CHECKSIG | Equality is checked between the top two stack items. |
| true | Empty. | Signature is checked for top two stack items. |
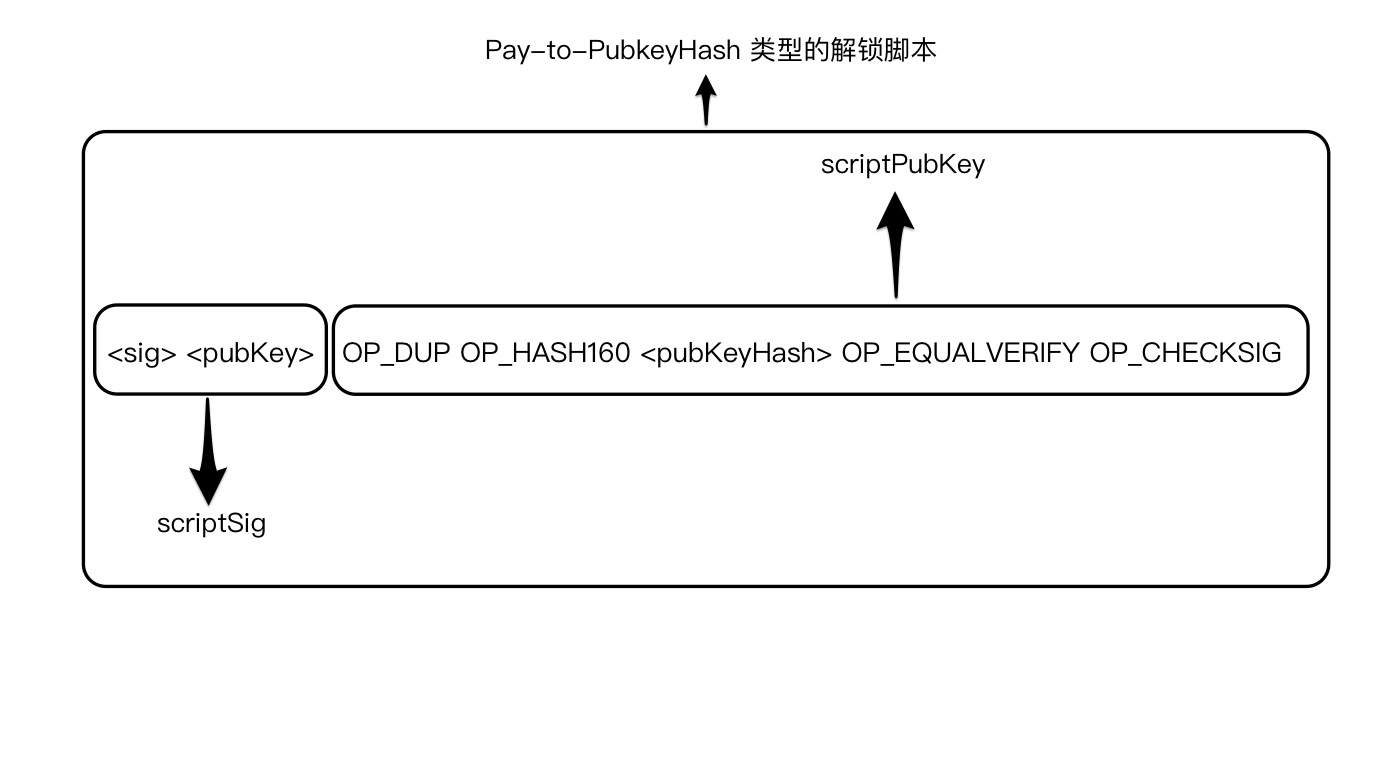
类似于做一道填空题, 上图中尖括号里面的内容是需要我们自行填进去的. 一般来说先有 scriptPubKey, 然后有对应的 scriptSig, 我们可以把 scriptPubKey 比喻为问题, scriptSig 比喻为应答, 先有问题,然后有应答, 但是在比特币系统中会出现没有 “问题” 的 “应答”, 比如创世交易中的 scriptSig 就没有对应的 scriptPubkey. 我们知道比特币是发送到一个目标 address 的, 对目标 address 进行 Base58 解码就可以得到 pubKeyHash, 将 pubKeyHash 填入到 OP_DUP OP_HASH160 <pubKeyHash> OP_EQUALVERIFY OP_CHECKSIG 中, 我们就做出了一个 scriptPubKey. 严谨起见,我们将使用真实的比特币交易数据来验证程序的可靠性.
我们使用两笔真实的比特币交易 Tx-36b6 和 Tx-d37d 作为验证对象.
简单的说 Tx-36b6 是 Tx-d37d 的上家, 这两笔交易的结构比较简单,特别是 Tx-d37d 只包含一个来自于 Tx-36b6 的输入, 适合我们做数据验证.
Tx-36b6 有两个 vout, 其中一个 vout 指向了 Tx-d37d, 这个 vout 的 scriptPubkey 是 OP_DUP OP_HASH160 c73e88dfa45a940bbec4f5654b910254e8b5d7be OP_EQUALVERIFY OP_CHECKSIG
Tx-36b6 的 txid 是 eaa98ab6900b5fff63c3d7b2ea122f4244301c290c76b4d1296f299acdc036b6
vout: [
{
value: "0.01844350",
n: 0,
scriptPubKey: {
hex: "76a914d732696463b5279021e0ccd78becdbeb98cb692b88ac",
asm: "OP_DUP OP_HASH160 d732696463b5279021e0ccd78becdbeb98cb692b OP_EQUALVERIFY OP_CHECKSIG",
addresses: [
"1LcrfuizJqEbyMSmiDabzn5WBfhV2fNevV"
],
type: "pubkeyhash"
},
spentTxId: "5ed38087986beb55b142a66dc1fd41af7d26fd4d1d652875517387bb55fb2d96",
spentIndex: 2,
spentHeight: 456006
},
{
value: "0.00050000",
n: 1,
scriptPubKey: {
hex: "76a914c73e88dfa45a940bbec4f5654b910254e8b5d7be88ac",
asm: "OP_DUP OP_HASH160 c73e88dfa45a940bbec4f5654b910254e8b5d7be OP_EQUALVERIFY OP_CHECKSIG",
addresses: [
"1KAWPAD8KovUo53pqHUY2bLNMTYa1obFX9"
],
type: "pubkeyhash"
},
spentTxId: "1e4f607d33175aa3b0a854c7d494ee0eb0ac3f0fc0a759ad1ddf88efbe8cd37d",
spentIndex: 0,
spentHeight: 462187
}
]
Tx-d37d 只有一个 vin, 这个 vin 来自于 Tx-36b6.
Tx-d37d 的 txid 是 1e4f607d33175aa3b0a854c7d494ee0eb0ac3f0fc0a759ad1ddf88efbe8cd37d
vin: [
{
txid: "eaa98ab6900b5fff63c3d7b2ea122f4244301c290c76b4d1296f299acdc036b6",
vout: 1,
scriptSig: {
asm: "304402207f9837b1e2a45e1e7f8054cb841af7e62fd40bf1a9becbebf38e9befe605905b02201fd0d11e48183c0b812f5fdecc36c0caf6fd1184d3ebd85192d711824c02f015[ALL] 04c4ae8574bd6a8a89af1fad3a945b14f6745cc998f544ab193ffc568b33598f2191dd06dd37c3b971f6f8452e84d86bcb82c29d7fb8787723ca08216a24051af3",
hex: "47304402207f9837b1e2a45e1e7f8054cb841af7e62fd40bf1a9becbebf38e9befe605905b02201fd0d11e48183c0b812f5fdecc36c0caf6fd1184d3ebd85192d711824c02f015014104c4ae8574bd6a8a89af1fad3a945b14f6745cc998f544ab193ffc568b33598f2191dd06dd37c3b971f6f8452e84d86bcb82c29d7fb8787723ca08216a24051af3"
},
sequence: 4294967294,
n: 0,
addr: "1KAWPAD8KovUo53pqHUY2bLNMTYa1obFX9",
valueSat: 50000,
value: 0.0005,
doubleSpentTxID: null
}
]
我们验证的方式如下:
1. 解码 1KAWPAD8KovUo53pqHUY2bLNMTYa1obFX9 然后做一个 scriptPubKey, 验证这个 scriptPubKey 能否和 OP_DUP OP_HASH160 c73e88dfa45a940bbec4f5654b910254e8b5d7be OP_EQUALVERIFY OP_CHECKSIG 一样.
#include <stdio.h>
#include <stdlib.h>
#include <unistd.h>
#include <errno.h>
#include <string.h>
#include <time.h>
#include "kyk_utils.h"
#include "kyk_script.h"
#define KYK_SC_MAX_LEN 1000
int main()
{
unsigned char sc[KYK_SC_MAX_LEN];
char *addr = "1KAWPAD8KovUo53pqHUY2bLNMTYa1obFX9";
size_t len;
/* 从比特币地址中提取 pay-to-pubkey-hash 脚本 */
len = p2pkh_sc_from_address(sc, addr);
kyk_print_hex("scriptPubKey Hex ", sc, len);
}
构造 pay-to-pubkey-hash 脚本的逻辑可以在 kyk_script.c 文件中查看.
$ make kyk_sc_pubkey_test && ./kyk_sc_pubkey_test.out
输出: “scriptPubKey Hex : 76a914c73e88dfa45a940bbec4f5654b910254e8b5d7be88ac” 和 Tx-36b6 的第 2 个 vout 的 scriptPubKey Hex 是一样的.

2. 将上面我们做出的 scriptPubKey 和 Tx-d37d vin 中的 scriptSig 合并起来运行, 验证是否能够得到 true 值.
验证代码可以通过 kyk_exe_p2pkh_sc_test.c 查看. 在调试 kyk_exe_p2pkh_sc_test.c 的时候我发现 Script 的 stack 中的 sig 数据的尾端的一个字节固定为 0x01, 一开始很疑惑, 后来通过查询 https://en.bitcoin.it/wiki/OP_CHECKSIG, 明白了这个字节表示的是 1 byte hash-type, 并且知道了 Signature format is [<DER signature> <1 byte hash-type>]. Hashtype value is last byte of the sig, 所以通过真实的比特币数据验证程序是非常重要的,让我们可以发现很多比特币设计的套路.
Hashtype Values:
| Name | Value |
|---|---|
| SIGHASH_ALL | 0x00000001 |
| SIGHASH_NONE | 0x00000002 |
| SIGHASH_SINGLE | 0x00000003 |
| SIGHASH_ANYONECANPAY | 0x00000080 |
pay-to-pubkey-hash 脚本有两个核心逻辑:
1. 将来自于 scriptSig 的 <pubKey> 和来自于 scriptPubKey 的 <pubKeyHash> 进行比较看是否匹配, 而 address 是通过对 <pubKeyHash> 进行 base58 编码得到的,所以 address 等价于 <pubKeyHash>,所以此逻辑可以概括为验证 <pubKey> 是否和 address 匹配;
2. 将来自于 scriptSig 的 <sig> <pubKey> 进行 OP_CHECKSIG 操作看是否返回 true 值, 下面是 OP_CHECKSIG 的逻辑
An array of bytes is constructed from the serialized txCopy appended by four bytes for the hash type.
This array is sha256 hashed twice, then the public key is used to check the supplied signature against the hash.
The secp256k1 elliptic curve is used for the verification with the given public key.
上面的文字的简单解释就是: 首先 text = sha256(sha256(Tx + 4 bytes hash type)), 然后 ecdsa_signature_verify(sig, text, pubKey), text 是被签名对象,如果是使用 pubKey 对应的私钥签名的话, 那么 ecdsa_signature_verify(sig, text, pubKey) 将返回 true 值.
第 1 条逻辑保证了 <pubKey> 是来自比特币的持有人, 第 2 条逻辑保证了比特币持有人用自己的私钥对 Tx 进行了签名, 即 <sig> 也来自比特币持有人.
现在我们要学习下有关 sig 结构相关的知识, 有个术语 DER format 用来描述 sig 的结构, 知道了这个术语我们以后就可以通过 google 直接搜索 DER format 来 查找相关的资料.
https://bitcoin.stackexchange.com/questions/12554/why-the-signature-is-always-65-13232-bytes-long
A correct DER-encoded signature has the following form:
0x30: a header byte indicating a compound structure.
A 1-byte length descriptor for all what follows.
0x02: a header byte indicating an integer.
A 1-byte length descriptor for the R value
The R coordinate, as a big-endian integer.
0x02: a header byte indicating an integer.
A 1-byte length descriptor for the S value.
The S coordinate, as a big-endian integer.
Where initial 0x00 bytes for R and S are not allowed, except when their first byte would otherwise be above 0x7F (in which case a single 0x00 in front is required). Also note that inside transaction signatures, an extra hashtype byte follows the actual signature data.
我画了一张图以帮助读者更加直观地理解上面的文字.
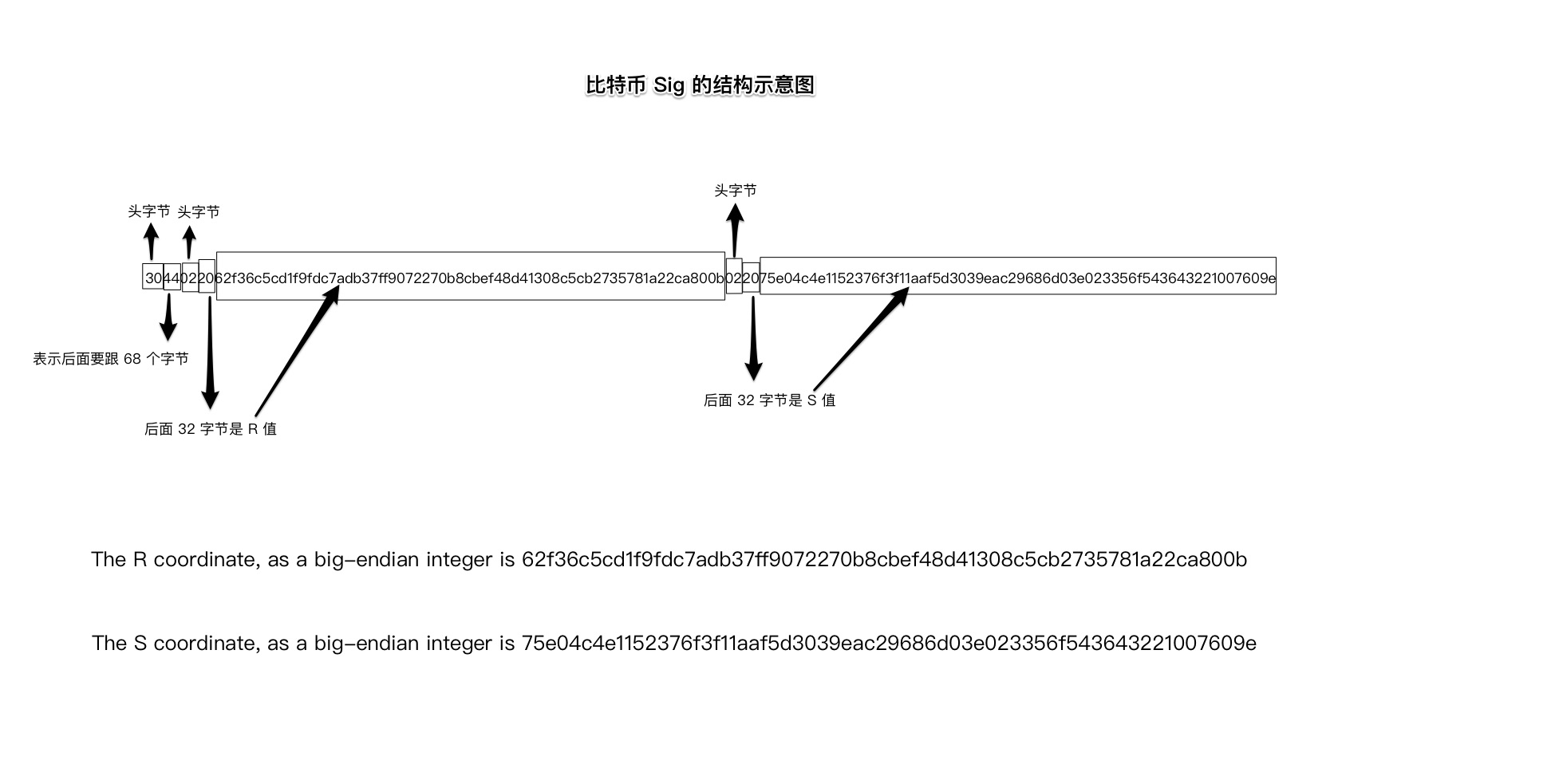
我们写一个小程序来获取 sig 的 R 值和 S 值.
#include <stdio.h>
#include <stdlib.h>
#include <unistd.h>
#include <errno.h>
#include <string.h>
#include <time.h>
#include <openssl/bn.h>
#include <openssl/ec.h>
#include <openssl/obj_mac.h>
#include <openssl/ecdsa.h>
#include "kyk_utils.h"
int main()
{
char *sig_hex = "3044022062f36c5cd1f9fdc7adb37ff9072270b8cbef48d41308c5cb2735781a22ca800b022075e04c4e1152376f3f11aaf5d3039eac29686d03e023356f543643221007609e";
uint8_t *sig;
const uint8_t *sig_cpy;
size_t sig_len;
ECDSA_SIG *signature;
sig = kyk_alloc_hex(sig_hex, &sig_len);
sig_cpy = sig;
signature = d2i_ECDSA_SIG(NULL, &sig_cpy, sig_len);
printf("R : %s\n", BN_bn2hex(signature->r));
printf("S : %s\n", BN_bn2hex(signature->s));
}
$ make sig_parse_test & ./sig_parse_test.out, 输出:
R : 62F36C5CD1F9FDC7ADB37FF9072270B8CBEF48D41308C5CB2735781A22CA800B
S : 75E04C4E1152376F3F11AAF5D3039EAC29686D03E023356F543643221007609E
输出的 R 和 S 值和上图给出的 R 和 S 值是一样的.
在 kyk_exe_p2pkh_sc_test.c 这个程序中当前交易即要被签名的交易是 Tx-d37d, 为了让读者更清楚地理解比特币的签名过程,我画了一张图来描述这一签名过程.

上图中的数据是真实的,其中,
上家交易是 https://blockexplorer.com/api/tx/eaa98ab6900b5fff63c3d7b2ea122f4244301c290c76b4d1296f299acdc036b6
下家交易是 https://blockexplorer.com/api/tx/1e4f607d33175aa3b0a854c7d494ee0eb0ac3f0fc0a759ad1ddf88efbe8cd37d
kyk_exe_p2pkh_sc_test.c 程序主要依赖两个文件: kyk_script.c 和 kyk_ser.c.
1. kyk_script.c 实现了验证 pay-to-pubkey-hash 的功能, 目前也只实现了这个功能,但是容易对其进行扩展以支持验证其他类型的脚本.
下面是用来运行比特币脚本的入口代码,
int kyk_run_sc(uint8_t *sc, size_t sc_len, uint8_t *tx, size_t tx_len)
{
struct kyk_sc_stack stk;
uint8_t opcode;
size_t count = 0;
init_sc_stack(&stk);
while(count < sc_len){
opcode = *sc;
if(is_sc_na_const(opcode) == 1){
sc++;
count += 1;
kyk_sc_stack_push(&stk, sc, opcode);
sc += opcode;
count += opcode;
} else {
switch (opcode){
case OP_DUP:
sc++;
count += 1;
kyk_sc_op_dup(&stk);
break;
case OP_HASH160:
sc++;
count += 1;
kyk_sc_op_hash160(&stk);
break;
case OP_EQUALVERIFY:
sc++;
count += 1;
if(kyk_sc_op_eq_verify(&stk) < 1){
free_sc_stack(&stk);
return 0;
}
break;
case OP_CHECKSIG:
sc++;
count += 1;
if(kyk_sc_op_checksig(&stk, tx, tx_len) < 1){
free_sc_stack(&stk);
return 0;
}
break;
default:
fprintf(stderr, "Invalid Op Code: %x\n", opcode);
return 0;
break;
}
}
}
free_sc_stack(&stk);
return 1;
}
2. kyk_ser.c 实现了序列化交易数据的功能
我们可以用它方便地序列化交易数据, 并且不用去记忆相关数据的字节大小,字节序(little-endian 或者 big-endian)等底层信息.
uint8_t unsig_tx[1000];
uint8_t *utx_cpy = unsig_tx;
kyk_tx_inc_ser(&utx_cpy, "version-no", 2);
kyk_tx_inc_ser(&utx_cpy, "in-counter", 1);
kyk_tx_inc_ser(&utx_cpy, "pre-tx-hash:hex", "b636c0cd9a296f29d1b4760c291c3044422f12eab2d7c363ff5f0b90b68aa9ea");
kyk_tx_inc_ser(&utx_cpy, "pre-txout-inx", 1);
kyk_tx_inc_ser(&utx_cpy, "txout-sc-len", 0x19);
kyk_tx_inc_ser(&utx_cpy, "txout-sc-pubkey:hex", "76a914c73e88dfa45a940bbec4f5654b910254e8b5d7be88ac");
kyk_tx_inc_ser(&utx_cpy, "seq-no", 0xfeffffff);
kyk_tx_inc_ser(&utx_cpy, "out-counter", 1);
kyk_tx_inc_ser(&utx_cpy, "txout-value", 49500);
kyk_tx_inc_ser(&utx_cpy, "txout-sc-len", 0x19);
kyk_tx_inc_ser(&utx_cpy, "txout-sc-pubkey:hex", "76a9140b5b85548100b98164f7748f931b66eb1b1b0ec888ac");
kyk_tx_inc_ser(&utx_cpy, "lock-time", 461576);
运行 kyk_exe_p2pkh_sc_test 程序:
$ make kyk_exe_p2pkh_sc_test
$ ./kyk_exe_p2pkh_sc_test.out
script verified: true
我们成功验证了交易 Tx-d37d 对上家交易 Tx-36b6 的 pay-to-pubkey-hash 脚本.
2.2.2.4 生成 scriptSig
在 2.2.2.3 节的比特币签名过程示意图中,我们已经揭示了比特币签名的流程,在完成签名后,
len(sig + 1 byte hashtype) + sig + 1 byte hashtype + len(pubkey) + pubkey 就可以得到 scriptSig.
上面公式中 len 表示求长度,其单位为字节, + 不是做加法的意思, 而是拼接合并的意思.
在比特笔系统中还有一种特殊的 scriptSig, 它没有对应的 scriptPubKey, 这种 scriptSig 有自己的名字: coinbase.比如创世交易的 coinbase 是:
04ffff001d0104455468652054696d65732030332f4a616e2f32303039204368616e63656c6c6f72206f6e206272696e6b206f66207365636f6e64206261696c6f757420666f722062616e6b73
将上面的 coinbase 人肉解码,
04 - push the next 4 bytes to stack
FFFF001D - 4 bytes pushed, they appear to be the same as bits
01 - push the next 1 byte to stack
04 - 1 byte pushed
45 - push the next 69 bytes to stack
5468652054696D65732030332F4A616E2F32303039204368616E63656C6C6F72206F6E206272696E6B206F66207365636F6E64206261696C6F757420666F722062616E6B73 - pushed bytes
coinbase 不参与解锁脚本, 但是可以包含一些有意思的文字信息,比如运行下面的程序可以输出 The Times 03/Jan/2009 Chancellor on brink of second bailout for banks, 并且可以作为 nonce 的补充参与算力计算, 还可以用于标明是哪个矿场生产的区块.
#include <stdio.h>
#include <stdlib.h>
#include <unistd.h>
#include <errno.h>
#include <string.h>
#include "kyk_utils.h"
int main()
{
//char *cb_hex = "04ffff001d0104455468652054696d65732030332f4a616e2f32303039204368616e63656c6c6f72206f6e206272696e6b206f66207365636f6e64206261696c6f757420666f722062616e6b73";
char *cb_hex = "5468652054696d65732030332f4a616e2f32303039204368616e63656c6c6f72206f6e206272696e6b206f66207365636f6e64206261696c6f757420666f722062616e6b73";
uint8_t *cb;
uint8_t *cb_str;
size_t cb_len;
cb = kyk_alloc_hex(cb_hex, &cb_len);
cb_str = calloc(cb_len + 1, sizeof(uint8_t));
for(int i=0; i < cb_len; i++){
cb_str[i] = cb[i];
}
cb_str[cb_len] = '\0';
printf("%s\n", cb_str);
}
将创世交易的 coinbase 的前 8 个字节剔除,后面的内容是: The Times 03/Jan/2009 Chancellor on brink of second bailout for banks, 在构建我们自己的创世交易时我们也可以这样玩.
2.2.2.5 现在我们创造由自己掌控私钥的创世交易
创建创世交易的程序可以通过 kyk_gens_tx.c 查看.
$ make kyk_gens_tx
$ ./kyk_gens_tx.out
saved gens tx to gens-tx.bin successfully
Txid : b76d27da4abf50387dd70f5d6cc7e4df1d54722631cbbfdd292463df77aa0dbd
coinbase : 04ffff001d01043446726f6d20342f536570742f32303137204368696e61207374617274207375707072657373696e672074686520426974636f696e
创世交易会保存在 gens-tx.bin 这个文件中, 创世交易用到的私钥文件是: kyk-gens-priv.pem, 当然也可以自己生成私钥文件生成新的创世交易.
$ hexdump -C gens-tx.bin
00000000 01 00 00 00 01 00 00 00 00 00 00 00 00 00 00 00 |................|
00000010 00 00 00 00 00 00 00 00 00 00 00 00 00 00 00 00 |................|
00000020 00 00 00 00 00 ff ff ff ff 3c 04 ff ff 00 1d 01 |.........<......|
00000030 04 34 46 72 6f 6d 20 34 2f 53 65 70 74 2f 32 30 |.4From 4/Sept/20|
00000040 31 37 20 43 68 69 6e 61 20 73 74 61 72 74 20 73 |17 China start s|
00000050 75 70 70 72 65 73 73 69 6e 67 20 74 68 65 20 42 |uppressing the B|
00000060 69 74 63 6f 69 6e ff ff ff ff 01 00 e4 0b 54 02 |itcoin........T.|
00000070 00 00 00 19 76 a9 14 05 09 ba 51 4a fa 00 3a 67 |....v.....QJ..:g|
00000080 9a c7 b6 d7 c2 e2 c9 6b 37 d5 dc 88 ac 00 00 00 |.......k7.......|
00000090 00 |.|
00000091
或者使用一个 ruby 写的程序 parse_tx.rb 解析它:
$ ./parse_tx.rb gens-tx.bin
{
"hash":"b76d27da4abf50387dd70f5d6cc7e4df1d54722631cbbfdd292463df77aa0dbd",
"ver":1,
"vin_sz":1,
"vout_sz":1,
"lock_time":0,
"size":145,
"in":[
{
"prev_out":{
"hash":"0000000000000000000000000000000000000000000000000000000000000000",
"n":4294967295
},
"coinbase":"04ffff001d01043446726f6d20342f536570742f32303137204368696e61207374617274207375707072657373696e672074686520426974636f696e"
}
],
"out":[
{
"value":"100.00000000",
"scriptPubKey":"OP_DUP OP_HASH160 0509ba514afa003a679ac7b6d7c2e2c96b37d5dc OP_EQUALVERIFY OP_CHECKSIG"
}
]
}
我们把 coinbase 类型的交易称作创币交易, 在创币交易中, 上家交易的 Txid 的 32 个字节全部填充 0, 上家交易的输出索引的 4 个字节全部填充为 0xff, 这样其实表示创币交易没有上家交易, 也可以用这个两个特征判断 交易是否是创币交易.
我们几乎没有花费任何代价创建了由自己掌控地创世交易,并且给自己记录了 100 个比特币的进账, 下面我们需要引入算力,只有通过一定的算力计算才能记账,这种算力计算在比特币系统中称作挖矿, 这样我们就要开始进入一个新的主题了: 怎么构造区块?
3. 构造创世区块
学习新的东西特别是一些比较复杂的东西时应该先易后难, 循序渐进,所以我们从最简单的地方开始: 拆解区块。
3.1 拆解区块
拆解区块之前我们要做两个工作: 1. 了解我们要拆解对象的结构; 2. 准备待拆解的数据;
3.1.1 研究 Block 的结构和准备 Block 数据
Block structure
| Field | Description | Size |
|---|---|---|
| Magic no | value always 0xD9B4BEF9 | 4 bytes |
| Blocksize | number of bytes following up to end of block | 4 bytes |
| Blockheader | consists of 6 items | 80 bytes |
| Transaction counter | positive integer VI = VarInt | 1 - 9 bytes |
| transactions | the (non empty) list of transactions | <Transaction counter>-many transactions |
来源于: https://en.bitcoin.it/wiki/Block#Where_can_I_find_more_technical_detail.3F
Blocksize 的值指的是 sizeof(Blockheader) + sizeof(Transaction counter) + sizeof(transactions), 它不包括 Magic no 的 4 个字节,也不包括 Blocksize 的 4 个字节.
block 是以二进制的形式存储在文件中,这种文件称作 block file, 比如 blk000000.dat, 一个这样的文件中存储着成千上万个 block, 很自然地我们可以把 Magic no 当作各个 block 的分隔符, 当 Magic no 出现时即意味着要进入一个新的 block 的范围了.
Blockheader structure
| Field | Purpose | Updated when… | Size (Bytes) |
|---|---|---|---|
| Version | Block version number | You upgrade the software and it specifies a new version | 4 |
| hashPrevBlock | 256-bit hash of the previous block header | A new block comes in | 32 |
| hashMerkleRoot | 256-bit hash based on all of the transactions in the block | A transaction is accepted | 32 |
| Time | Current timestamp as seconds since 1970-01-01T00:00 UTC | Every few seconds | 4 |
| Bits | Current target in compact format | The difficulty is adjusted | 4 |
| Nonce | 32-bit number (starts at 0) | A hash is tried (increments) | 4 |
来源于: https://en.bitcoin.it/wiki/Block_hashing_algorithm
我们通过 Bitcoin Core 下载 block 数据:
在安装 Bitcoin Core 时,系统会提示你选择一个用于存放 block 数据的目录,选择一个你方便访问的目录即可。我们可以在同步一定量的数据后停止同步,因为 Bitcoin 的数据量非常大,我们只需要一小部分的数据用来做实验即可。
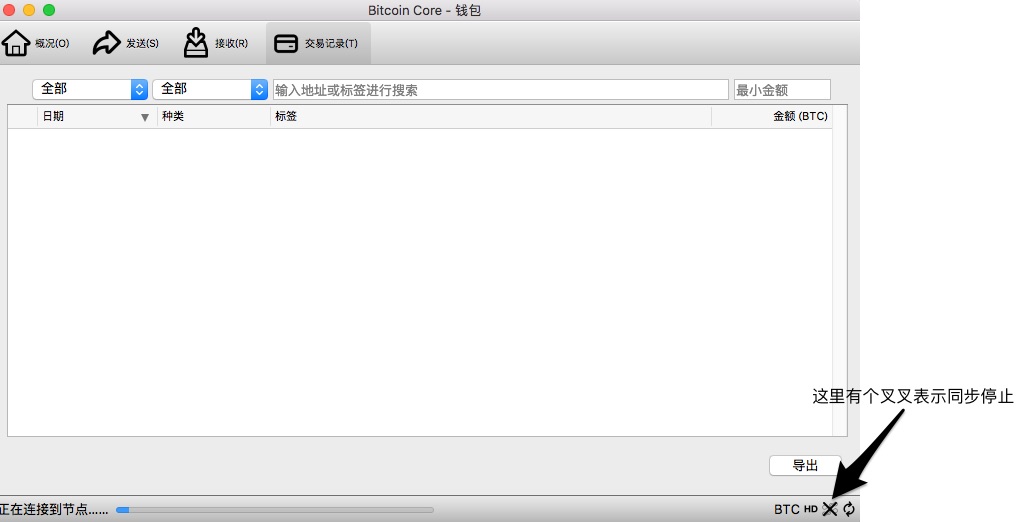
3.1.2 Block 拆解的程序细节
我们要注意到一个事实就是比特币系统的数据绝大部分是以 little-endian[byte-endian] 的形式序列化的, 即使运行比特币系统的主机是 big-endian, 比特币的大部分数据也会以
little-endian 的形式写入到文件中,或者以 little-endian 的形式打包成报文. 我们可以使用 hexdump 命令查看 block 文件.
$ hexdump -n 285 blk00000.dat
0000000 f9 be b4 d9 1d 01 00 00 01 00 00 00 00 00 00 00
0000010 00 00 00 00 00 00 00 00 00 00 00 00 00 00 00 00
0000020 00 00 00 00 00 00 00 00 00 00 00 00 3b a3 ed fd
0000030 7a 7b 12 b2 7a c7 2c 3e 67 76 8f 61 7f c8 1b c3
0000040 88 8a 51 32 3a 9f b8 aa 4b 1e 5e 4a 29 ab 5f 49
0000050 ff ff 00 1d 1d ac 2b 7c 01 01 00 00 00 01 00 00
0000060 00 00 00 00 00 00 00 00 00 00 00 00 00 00 00 00
0000070 00 00 00 00 00 00 00 00 00 00 00 00 00 00 ff ff
0000080 ff ff 4d 04 ff ff 00 1d 01 04 45 54 68 65 20 54
0000090 69 6d 65 73 20 30 33 2f 4a 61 6e 2f 32 30 30 39
00000a0 20 43 68 61 6e 63 65 6c 6c 6f 72 20 6f 6e 20 62
00000b0 72 69 6e 6b 20 6f 66 20 73 65 63 6f 6e 64 20 62
00000c0 61 69 6c 6f 75 74 20 66 6f 72 20 62 61 6e 6b 73
00000d0 ff ff ff ff 01 00 f2 05 2a 01 00 00 00 43 41 04
00000e0 67 8a fd b0 fe 55 48 27 19 67 f1 a6 71 30 b7 10
00000f0 5c d6 a8 28 e0 39 09 a6 79 62 e0 ea 1f 61 de b6
0000100 49 f6 bc 3f 4c ef 38 c4 f3 55 04 e5 1e c1 12 de
0000110 5c 38 4d f7 ba 0b 8d 57 8a 4c 70 2b 6b
000011d
-n 285 选项表示查看 block 文件的前 285 个字节的数据。
以 Magic no 为例, Magic no 的值固定为 0xD9B4BEF9, 它在 blk00000.dat 以 little-endian 的形式存储为: f9 be b4 d9, 它的高字节在低位, 与我们看到的顺序刚好相反。如果主机也是 little-endian, 那么我们用 fread 直接读取 f9 be b4 d9 即可, 如果我们的主机是 big-endian, 那么我们还需要将 fread 读取的值的字节调换个顺序. 我们可以通过下面的程序得到你所用电脑的 endian 类型:
#include <stdio.h>
int main()
{
int a;
char b;
a = 1;
b = *((char*)&a);
if(b)
{
printf("little endian\n");
}
else
{
printf("big endian\n");
}
}
我在 beej_pack.c 文件中扩展了 beej_unpack 方法使它支持以 little-endian 的形式 unpack 数据, 这样我们就不需要关心程序运行的主机的 endian 类型。当然通过判断主机的 endian 类型,然后针对性地做一些操作也是一种比较可靠的方法。
可以通过 parse_block.c 访问用于拆解 block 的程序, 这个程序的使用方法如下:
首先编译程序: make parse_block, 然后解析第 0 个 block,
$ ./parse_block.out -n 0 blk00000.dat
Magic no: d9b4bef9
Blocksize: 285
Version: 1
hashPrevBlock : 0000000000000000000000000000000000000000000000000000000000000000
hashMerkleRoot : 4a5e1e4baab89f3a32518a88c31bc87f618f76673e2cc77ab2127b7afdeda33b
Time: 1231006505
Bits: 486604799
Nonce: 2083236893
Transaction counter: 1
==========================================================================>block#0
解析 0 至第 10 个 block,
$ ./parse_block.out -n 10 blk00000.dat
为了更清晰地展现 block 的结构,这个程序没有解析 Tx.
3.2 算力计算
比特币系统的算力计算通俗地讲类似于掷色子。 假设我们做出了一种可以抛出 1 到 99 个数字的色子,并且这 99 个数字被抛出的概率是一样的都为 1/99, 那么抛出一个数小于 99 的概率是多少呢? 答案是 98/99 接近 100%, 我们可以认为这样的难度(difficulty[4]) 是 0, 抛出一个数小于 80 的概率是 79/99, 我们可以把这个难度记为 1, 于是有了第一个概念: difficulty_1_target, 这个概念的意思是抛出一个数小于 difficulty_1_target 的难度是 1, 目前我们设定 difficulty_1_target = 80,
现在提问,抛出一个数小于 10 的难度是多少呢? 答案是 8, 怎么算的呢? 通过下面的公式算出来的:
difficulty = difficulty_1_target / current_target
difficulty = 80 / 10 算出 difficulty 是 8, 其中的 10 是 current_target.
current_target 越小,difficulty 越大, difficulty 越大的意思是你要多抛几次色子,多耗费点你的力气,你才能达到目标, 当然有时候你的运气很好,可能抛一次就能达到目标,但是从概率的角度来看,这个 difficulty 确实是一种实实在在的难度。
比特币系统用的不是我们这种只有 1 到 99 个数字的色子,而是一种拥有有巨量数字的色子: (target is a 256 bit number), 当然原理是一样的,都是色子。
比特币使用 sha256 对 block header 进行 hash 计算, block header 中的 version, timestamp, prev_block 之类的数据都是固定的, 只有 nonce 可以变化(现在 coinbase 也可变化), 所以为了算出一个小于 target 的 hash 值,就要不断地增加 nonce 值,直到 hash 值小于 target, 这样 nonce 也就确定下来了.
这个链接 https://en.bitcoin.it/wiki/Block_hashing_algorithm 对比特币的算力计算原理和过程做了清晰详细的描述。
下面我们会用两个程序实际地演示比特币的算力计算. 第 1 个程序会对真实的 block 数据进行 hash 计算,以验证我们能够正确地计算 block 的 hash. 第 2 个程序会对真实的 block 数据进行 hash 计算, 目标是寻找到满足 target 的 nonce.
3.2.1 计算 block 的 hash
计算 block 的 hash 更准确的讲应该是 计算 block header 的 hash, 计算的公式是 SHA256(SHA256(Block_Header))[3], 那么 block 中的 transaction 有没有成为 hash 计算的参与者呢? 答案是肯定的, 这些 transaction 通过变成 Merkle root 间接地参与了 hash 计算. 我会在后面的章节中详细地描述 Merkle Trees[8].
可以通过 block_hash_test.c 访问代码, block_hash_test.c 使用的区块数据来自于比特币的创世区块[11].
#include <stdio.h>
#include <string.h>
#include <stdlib.h>
#include <openssl/sha.h>
#include "kyk_block.h"
#include "kyk_utils.h"
#include "kyk_sha.h"
int main()
{
struct kyk_blk_header blk_hd;
uint8_t hd_buf[1000];
size_t hd_len;
uint8_t dgst[SHA256_DIGEST_LENGTH];
blk_hd.version = 1;
kyk_parse_hex(blk_hd.pre_blk_hash, "0000000000000000000000000000000000000000000000000000000000000000");
kyk_parse_hex(blk_hd.mrk_root_hash, "4a5e1e4baab89f3a32518a88c31bc87f618f76673e2cc77ab2127b7afdeda33b");
blk_hd.tts = 1231006505;
blk_hd.bts = 486604799;
blk_hd.nonce = 2083236893;
hd_len = kyk_seri_blk_hd(hd_buf, &blk_hd);
kyk_dgst_hash256(dgst, hd_buf, hd_len);
kyk_reverse(dgst, sizeof(dgst));
kyk_print_hex("block hash", dgst, sizeof(dgst));
}
执行程序:
$ make block_hash_test
$ ./block_hash_test.out
block hash: 000000000019d6689c085ae165831e934ff763ae46a2a6c172b3f1b60a8ce26f
输出的结果和比特币创世区块[11]的 hash 是一致的.
3.2.2 找到符合要求的 nonce
区块头的 Bits 字段中存储着 target[12], 当然这个 target 是经过编码的,需要通过解码得到真实的 target 值,然后利用下面的公式:
difficulty = difficulty_1_target / current_target
就能算出当前区块的 difficulty. 由于 target 是一个 256 bits的大数(big number), 在 c 语言中处理这种类型的大数我们需要使用专门的 big number 库,比如我们可以使用 GNU MP[13].
如果 Bits 是 0x1b0404cb, 则可以通过下面的计算得到其对应的 target:
0x0404cb * 2*(8(0x1b - 3)) = 0x00000000000404CB000000000000000000000000000000000000000000000000
熟悉位操作的读者很容易将上面等式的左边转换为: 0x0404cb << (8 * (0x1b -3)), 它的意思是将 0x0404cb 向左位移 8 * (0x1b -3) = 192 = 24 个字节, 这种转换有助于以后我们将一个 target 编码为一个 Bits.
现在我们利用 GNU MP[13] 库写一个程序来实现这一过程,
#include <stdio.h>
#include <string.h>
#include <stdlib.h>
#include <gmp.h>
#define DLT1_TARGET_HEX_STR "0x00000000FFFF0000000000000000000000000000000000000000000000000000"
void bts2target(uint32_t bts, mpz_t tg);
uint32_t bts2dlt(uint32_t bts);
/*
* 0x1b0404cb
* 0x0404cb * 2**(8*(0x1b - 3)) = 0x00000000000404CB000000000000000000000000000000000000000000000000
*/
int main()
{
uint32_t bts = 0x1b0404cb;
//uint32_t bts = 0x1d00ffff;
uint32_t dlt;
mpz_t tg;
mpz_init(tg);
mpz_set_ui(tg, 0);
bts2target(bts, tg);
dlt = bts2dlt(bts);
gmp_printf("0x%02x => target is: 0x%Zx\n", bts, tg);
gmp_printf("0x%02x => difficulty is: %u\n", bts, dlt);
}
uint32_t bts2dlt(uint32_t bts)
{
uint32_t res;
mpz_t tg, dlt1_tg, q;
mpz_init(tg);
mpz_init(dlt1_tg);
mpz_init(q);
mpz_set_ui(tg, 0);
mpz_set_str(dlt1_tg, DLT1_TARGET_HEX_STR, 0);
bts2target(bts, tg);
mpz_cdiv_q(q, dlt1_tg, tg);
res = mpz_get_ui(q);
mpz_clear(tg);
mpz_clear(dlt1_tg);
mpz_clear(q);
return res;
}
void bts2target(uint32_t bts, mpz_t tg)
{
uint8_t ep = bts >> 24;
uint32_t mt = bts & 0xffffff;
mpz_ui_pow_ui(tg, 2, 8 * (ep - 3));
mpz_mul_ui(tg, tg, mt);
}
编译运行程序:
$ make bits_to_target
$ ./bits_to_target.out
0x1b0404cb => target is: 0x404cb000000000000000000000000000000000000000000000000
0x1b0404cb => difficulty is: 16308
人肉解码 bits 得到 target
现在我们尝试下手工解码 0x1b0404cb, 0x1b = 27, 27 - 3 = 24, 24 * 2 = 48, 我们在 0404cb 后面追加 48 个零就得到了 0x404cb000000000000000000000000000000000000000000000000, 其实在后面追加 48 个 f 也可以.
期望多长的时间生成一个 block ?
下面的公式可以计算生成一个 block 的平均时间,
time = difficulty * 2**32 / hashrate
上面公式的详细推导过程可以在 https://en.bitcoin.it/wiki/Difficulty [4] 找到.
上面的 hashrate 表示的是每秒钟运行 hash 运算的次数, 如果 hashrate 是 1Ghash/s, difficulty 是 20000, 那么生成一个 block 将花费,
python -c "print 20000 * 2**32 / 10**9 / 60 / 60.0"
23.85
23.85 小时.
Bitcoin Mining Hardware Jargon, 比特币矿机行话[15]
- Kilohash or KH/s = thousands of H/s
- Megahash or MH/s = millions/s = 10 ** 6 / s
- Gigahash or GH/s = billions/s = 10 ** 9 / s
- Terahash or TH/s = trillions/s = 10 ** 12 / s
- Petahash or PH/s = quadrillions/s = 10 ** 15 / s
上面的这些大数都可以在 https://en.wikipedia.org/wiki/Names_of_large_numbers [16] 找到对应的定义。
比特币的算力运算现在都是在专用都矿机上进行的,所以了解下专用矿机的各项指标对我们以后改进比特币也许会有帮助,下面是一组 2016 年的主流矿机的指标数据。
数据来源于 https://99bitcoins.com/2016-bitcoin-mining-hardware-comparison/ [15],
| Avalon6 | AntMiner S7 | AntMiner S9 | |
|---|---|---|---|
| Hashrate1 | 3.5 TH/s | 4.73 TH/s | 11.8 – 14 TH/s |
| Power Usage2 | 1050 Watts | 1350 Watts | 1350 Watts |
| Power Efficiency2 | 0.29 Joule per GH | 0.25 Joule per GH | 0.1 Joule per GH |
| Controller Separate | (RasPi) | Built-in | Built-in |
| Noise @ 4ft/1.2m2 | 55 dB | 62 dB | 70 dB |
| Chip Process | 28nm | 28nm | 16nm |
| Price New2,3 | $550 (Canaan) | $440 (Bitmain) | $1831 – 2016 (Bitmain) |
| Price Used2,3 | $360 – $875 | $440 – $674 | n/a |
| Profitability4 | Possible | Marginal | Plausible |
| Break-even point5 | 7 years | 2.6 years | 0.9 years |
目前主流的矿机算力都是 TH/s, 普通用户只能通过购买的方式才能得到比特币。但是在这篇文章中我们可以自行设定 difficulty 为一个较小的数,或者将 nonce 设置为一个接近目标 nonce(因为已经挖出的 block 的 nonce 都是已知的) 的数,这样我们就可以在自己的电脑上”挖矿”了.
在程序 block_nonce_test.c 中实现了一个非常简单的挖矿过程, 虽然它在复杂程度和效率方面和专业挖矿相比是有巨大差异的, 但是它的原理和矿机挖矿是一样的,都是不断增加 nonce, 直到算出的 hash 值小于 target.
#include <stdio.h>
#include <string.h>
#include <stdlib.h>
#include <openssl/sha.h>
#include "kyk_block.h"
#include "kyk_utils.h"
#include "kyk_sha.h"
#include "kyk_difficulty.h"
#include "beej_pack.h"
int main()
{
struct kyk_blk_header blk_hd;
uint8_t hd_buf[1000];
size_t len;
uint8_t dgst[SHA256_DIGEST_LENGTH];
blk_hd.version = 1;
kyk_parse_hex(blk_hd.pre_blk_hash, "0000000000000000000000000000000000000000000000000000000000000000");
kyk_parse_hex(blk_hd.mrk_root_hash, "4a5e1e4baab89f3a32518a88c31bc87f618f76673e2cc77ab2127b7afdeda33b");
blk_hd.tts = 1231006505;
blk_hd.bts = 486604799;
/*
* 在已经知道目标 nonce 的情况下, 如果从 0 开始跑计算,需要跑 20 多亿次(准确地说是 40 多亿次) sha256 计算,在没有矿机的情况下,这个实验就没有办法在较短的时间内做下去了
* 所以将 nonce 设置为一个较大的数,这样只要跑 1 千万次(准确地说是 2 千万次, 因为比特币系统中算一次 hash 要跑两次 sha256 计算) sha256 计算就能得到结果.
*/
blk_hd.nonce = 2082236893;
uint32_t dlt;
mpz_t tg, hs;
mpz_init(tg);
mpz_set_ui(tg, 0);
mpz_init(hs);
mpz_set_ui(hs, 0);
/* bts to difficulty */
dlt = kyk_bts2dlt(blk_hd.bts);
/* bts to target */
kyk_bts2target(blk_hd.bts, tg);
gmp_printf("0x%02x => target is: 0x%Zx\n", blk_hd.bts, tg);
gmp_printf("0x%02x => difficulty is: %u\n", blk_hd.bts, dlt);
len = kyk_seri_blk_hd_without_nonce(hd_buf, &blk_hd);
do{
beej_pack(hd_buf+len, "<L", blk_hd.nonce);
kyk_dgst_hash256(dgst, hd_buf, KYK_BLK_HD_LEN);
kyk_reverse(dgst, SHA256_DIGEST_LENGTH);
mpz_import(hs, SHA256_DIGEST_LENGTH, 1, 1, 1, 0, dgst);
if(mpz_cmp(hs, tg) > 0){
blk_hd.nonce += 1;
} else {
break;
}
} while(1);
kyk_print_hex("got block hash", dgst, sizeof(dgst));
printf("got nonce: %u\n", blk_hd.nonce);
}
上面程序的 block 数据来自比特币的创世区块[11], 编译和运行程序:
$ make block_nonce_test
$ ./block_nonce_test.out
0x1d00ffff => target is: 0xffff0000000000000000000000000000000000000000000000000000
0x1d00ffff => difficulty is: 1
got block hash: 000000000019d6689c085ae165831e934ff763ae46a2a6c172b3f1b60a8ce26f
got nonce: 2083236893
3.3 打包创世交易, 构造创世区块
我们知道比特币的每一个区块中都包含着交易, 虽然在比特币初期的时候,很多区块只包含了一笔交易, 但是后期随着比特币的日益火热,矿工的激烈竞争, 很多区块包含着成千上万笔交易, 为了归纳一个区块中大规模的交易,并生成整个交易集合的数字指纹,比特币系统引入了 Merkle 树[19].
3.3.1 Merkle 树的结构分析和代码实现
假设某个区块中有 T1, T2, T3, T4, T5 笔交易, 简单的做法是把 T1 至 T5 笔交易合并起来,然后做一个数字指纹, 比如 SHA256(SHA256(T1 + T2 + T3 + T4 + T5)), 其中 + 表示拼接的意思. 这样的做法有一些缺点不太适合比特币系统, 我们会在后面讲述为什么不适用于比特币系统。现在我们用 Merkle 树来实现这归纳交易的功能,其计算过程如下所示:
- H[1][1] = Hash(T1)
- H[1][2] = Hash(T2)
- H[1][3] = Hash(T3)
- H[1][4] = Hash(T4)
- H[1][5] = Hash(T5)
- H[2][1] = Hash(H[1][1] + H[1][2])
- H[2][2] = Hash(H[1][3] + H[1][4])
- H[2][3] = Hash(H[1][5] + H[1][5])
- H[3][1] = Hash(H[2][1] + H[2][2])
- H[3][2] = Hash(H[2][3] + H[2][3])
- H[4][1] = Hash(H[3][1] + H[3][2])
Hash 表示两次 SHA256计算, H[i][j] 表示一个节点, 其中 i 表示节点所在的层数, j 表示节点的序号, 第 1 层的节点是直接对交易进行 Hash 计算得到的,第 i(i > 1) 层的节点是对第 i - 1 层的每 2 个节点依次进行 Hash 计算得到的, 如果尾节点没有匹配的节点,则对尾节点进行一个拷贝,然后再合并拷贝的节点进行 Hash 计算.
我们画张图对上述的计算过程进行更加直观地描述,
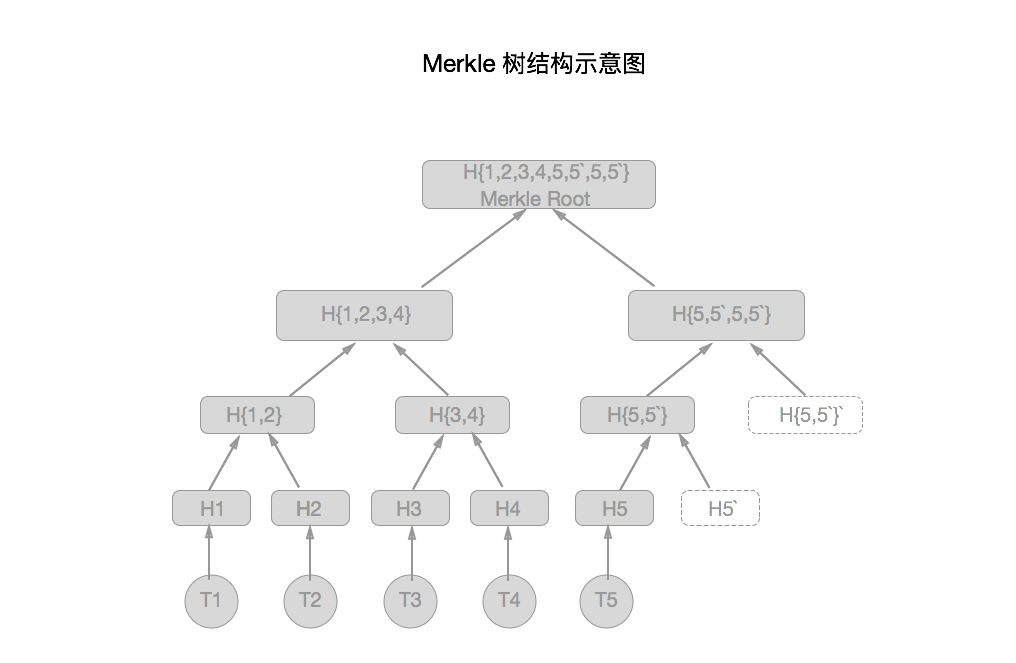
Merkle 树的代码实现可以通过 kyk_mkl_tree.h 和 kyk_mkl_tree.c 查看.
为了验证程序的正确性, 我写了下面的测试代码:
- kyk_mkl_tree1_test.c 测试了生成包含 1 笔交易的 Merkly 树
#include <stdio.h>
#include <string.h>
#include <stdlib.h>
#include "kyk_utils.h"
#include "kyk_mkl_tree.h"
/* 数据来源于: https://webbtc.com/block/000000000019d6689c085ae165831e934ff763ae46a2a6c172b3f1b60a8ce26f.json */
/* mrkl_tree: [ */
/* "4a5e1e4baab89f3a32518a88c31bc87f618f76673e2cc77ab2127b7afdeda33b" */
/* ] */
void build_tx_buf_from_hex(struct kyk_tx_buf *tx_buf, const char *hexstr);
int main()
{
char *tx1_hex = "01000000010000000000000000000000000000000000000000000000000000000000000000ffffffff4d04ffff001d0104455468652054696d65732030332f4a616e2f32303039204368616e63656c6c6f72206f6e206272696e6b206f66207365636f6e64206261696c6f757420666f722062616e6b73ffffffff0100f2052a01000000434104678afdb0fe5548271967f1a67130b7105cd6a828e03909a67962e0ea1f61deb649f6bc3f4cef38c4f35504e51ec112de5c384df7ba0b8d578a4c702b6bf11d5fac00000000";
struct kyk_tx_buf buf_list[1];
struct kyk_mkltree_level *leaf_level;
struct kyk_mkltree_level *root_level;
build_tx_buf_from_hex(buf_list, tx1_hex);
leaf_level = create_mkl_leafs(buf_list, sizeof(buf_list) / sizeof(buf_list[0]));
root_level = create_mkl_tree(leaf_level);
kyk_print_mkl_tree(root_level);
}
void build_tx_buf_from_hex(struct kyk_tx_buf *tx_buf, const char *hexstr)
{
tx_buf -> bdy = kyk_alloc_hex(hexstr, &tx_buf -> len);
}
-
kyk_mkl_tree2_test.c 测试了生成包含 2 笔交易的 Merkly 树
-
kyk_mkl_tree6_test.c 测试了生成包含 6 笔交易的 Merkly 树
-
kyk_mkl_tree15_test.c 测试了生成包含 15 笔交易的 Merkly 树
-
kyk_mkl_tree32_test.c 测试了生成包含 32 笔交易的 Merkly 树
-
kyk_mkl_tree777_test.c 测试了生成包含 777 笔交易的 Merkly 树
现在我们编译运行 kyk_mkl_tree777_test.c, 过程如下:
$ make kyk_mkl_tree777_test
$ ./kyk_mkl_tree777_test.out
Level 11 (Merkle Root): 64661f58773c0adc28609866fe3942c0b1cdb4cb99a0602cee2903f3f2b9f35a
777 笔交易生成的 Merkle 树一共有 11 层, 它的 Root 是 64661f58773c0adc28609866fe3942c0b1cdb4cb99a0602cee2903f3f2b9f35a, 我们可以通过链接: https://blockexplorer.com/api/block/00000000000000001544f99d2e133956f5352feabba910ff64d0d87b16daa26c 核实下 Root 是否正确。
比特币系统中的 Merkle 树的计算其实包含有一些很隐晦的细节,这些细节很重要,它们会影响到整个计算结果的正确性, 但是比特币的文档好像没有对这些细节做出描述,当然比特币庞杂的源代码中肯定包含了这些细节,于是我画了一张图用于描述比特币系统中 Merkle 树的计算过程, 图中包含了那些隐晦的细节。
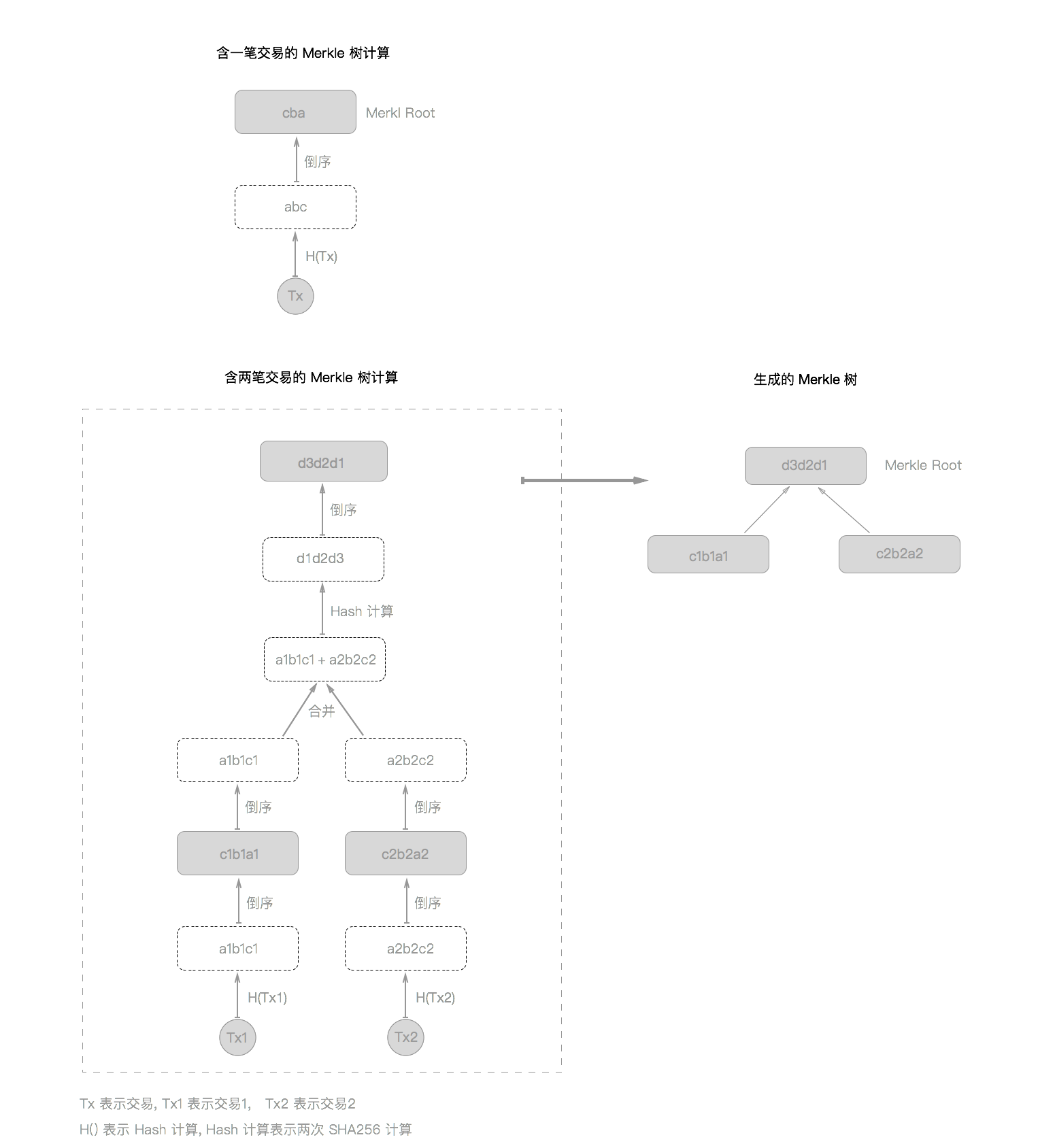
下图是包含三笔交易的 Merkle 树的计算过程,其中涉及到了孤节点的复制细节,
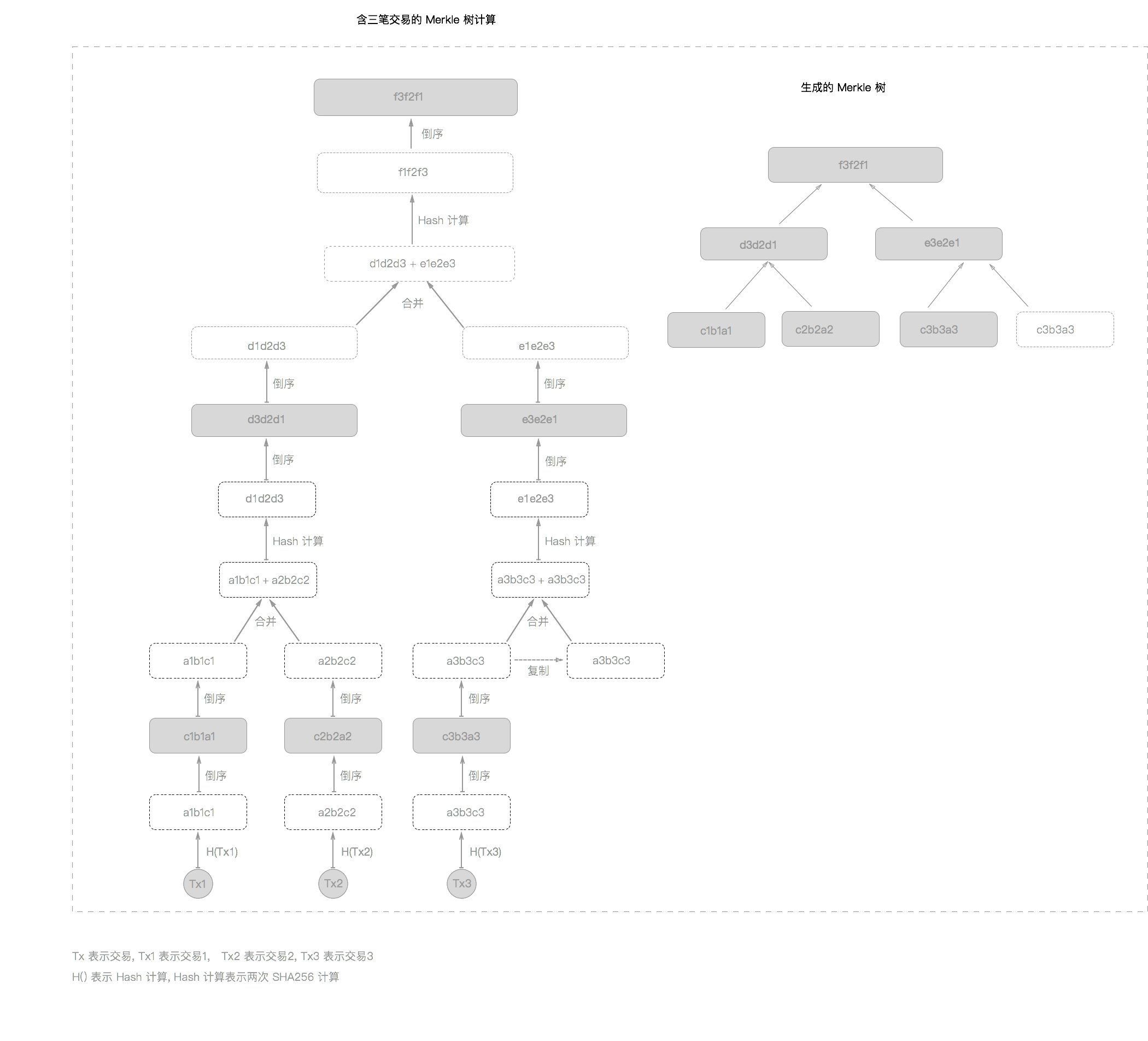
3.3.2 在比特币系统中, Merkle 树起到了什么作用
在比特币系统中, Merkle 树的叶子节点存储的是交易 ID 即 Txid, 所谓的叶子节点即没有分支的,通过对单个 Tx 进行 Hash 计算得到的那个节点, 它们属于 Merkle 树的第一层(从下往上数, root 节点属于顶层)。 通过比对 Root 节点和叶子节点我们能够验证交易数据是否正确可信, 那么为什么 Merkly 树能够验证数据正确可信呢? 要知道比特币是去中心化的,每个人都可以冒充成一个可信节点发送伪造的交易数据。为了回答这个问题,我们要好好聊聊比特币区块链的不可篡改性. 在 2017年8月1日发布了一种新的加密货币叫 BCC, 全称 Bitcoin Cash, 从名字来看这种货币和比特币很有关系, 事实上也是如此, 下面对 BCC 的简介摘录于 http://www.qukuaiwang.com.cn/szhb/2284.html:
简单来说,BCC是比特币的一种硬分叉产生的币,它修改了比特币的代码,支持大区块,并且不包含Segwit。BCC的前世就是比特币,分叉之前它存储的区块链中的数据以及运行的软件是和所有比特币节点兼容的,而到了分叉那一刻以后,它开始执行新的代码,打包大区块,这样就在链上形成了一个硬分叉。目前BCC还是一个期货,将于8月1日正式分叉成为一个新币种。——BCC是根据Bitcoin ABC方案产生的区块链资产,Bitcoin ABC方案为保持协议稳定简单,去除了Segwit功能,支持将区块大小提升至8M,是链上扩容的技术路线。Bitcoin ABC代码基于比特币协议的稳定版本进行了改进,其认为不包含Segwit将具有更大的稳定性、安全性、鲁棒性,是现行比特币协议和比特币系统的备份,BCC将从2017年8月1日20:20开始挖矿。
上面的话还可以再简单点: 中本聪背书 + Bitcoin ABC方案 + 矿场背书 = Bitcoin Cash, 中本聪背书的意思是继承了比特币原有的区块链, Bitcoin ABC方案指的是增加了一些和原来比特币不同的特性, 矿场背书指的是要有大型的矿场为这种新币生成新区块。
由于 BCC 只是继承了比特币原有的区块链,它并没有改动比特币区块链的任何数据(其实也没有办法改),所以 BCC 发布后,原先拥有比特币的人都可以在 BCC 的区块链上自动拥有相同数量的 BCC 币, BCC 网络继承了比特币网络的数据,但是两个网络是互相独立的,BCC 网络不会接受比特币的交易, 比特币网络也不会接受 BCC 的交易.
在比特币的世界里做出一种新的货币比较容易, 但是把新货币做成功很难.
我们可以把上面的公式改下,让它更抽象化: 大佬背书 + X 方案 + 金主背书 = X 币, 现在我要做一种新的货币叫它 VoidCoin, 我认识很多大佬,但是大佬都不认识我,所以我请中本聪背书, VoidCoin 的方案设定为: coinbase 的首个单词必须为 Void, 最后一步就是找土豪来支持这种货币了(推广,开矿等等), 当然如果你真的能够实现一种非常优秀的能够改变游戏规则的方案,金主会自动找上门来的。一句话总结:
比特币区块链上的每一个字节都凝聚了真金白银.
在比特币区块链上哪怕是有一个字节做了改变,都会引起连锁反应, 需要把区块链上的每一个区块的 Hash 都重新计算一遍, 这是需要花费巨大的算力才能做到的,在前面我已经论述了 比特币区块链上的每一个字节都凝聚了真金白银, 所以你也必须花费巨大的真金白银才能改变整条链, 并且这个”改变”貌似对你没有任何好处,因为比特币的非对称加密机制可以阻止你盗窃别人的比特币, 你只能开一条不被其他矿场认可的新链。这样的话即使你拥有巨大的算力,如果你稍微有理性的,你就不会去篡改比特币区块链, 所以说比特币从技术和动机两个方面打消了别人篡改比特币数据的念头。
前面我们已经论述了比特币区块链的不可篡改性, 我们把它当作一个定理:
比特币区块链不可篡改
比特币的区块链只能在链尾由矿工添加区块,如果比特币区块链被篡改了,我们就认为它不是比特币的区块链了,而是变成了另外一种区块链,当然如果有人破解了 SHA256 算法,那么比特币的区块链就被破坏了, 由此我们升级上面的定理为:
比特币区块链要么被破坏,但是不可被篡改
从比特币区块链的不可篡改定理出发,我们来论述 Merkle 树的作用。
在比特币网络中有一种 SPV[22] 节点, 这种节点有下面的特性:
connect to an arbitrary full node and download only the block headers. They verify the chain headers connect together correctly and that the difficulty is high enough
简单地来说 SPV 节点并不会下载全部的区块链数据,而只是下载区块头, 这些区块头组成的链我们称它为区块头链,这条链并不包括交易数据. 当前的某个时刻比特币区块链的高度是 489330, 一个区块头的大小是 80 个字节, 那么由区块头组成的链的大小大概是 37 M, 这和整个区块链动辄上几百 G 的数据相比少了很多很多。
由区块头组成的链在一定程度上和全节点上的区块链是等价的, 区块头组成的链同样遵守 比特币区块链不可篡改 的定理, 虽然区块头组成的链缺少了详细的交易数据,但是这些交易数据通过计算成 Merkle 树被归纳成了区块头中的 Merkle Root. 不可篡改定理保证了区块头中的 Merkle Root 是合法的。
场景一: SPV 节点下载某个区块的全部交易数据
因为比特币系统是一个去中心化的系统,它并没有一个所谓的中心服务器或中心节点, 所以我用比特币网络代替服务器或者中心这一术语.
当 SPV 节点请求比特币网络下载某个区块的交易数据时, 它首先会从比特币网络下载这个区块的 Merkle 树, SPV 节点会对这棵 Merkle 树做两步工作:
-
验证 Merkle 树的 Root 是否和自身区块头链中的 Merkle Root 相匹配;
-
按 Merkle 树的算法对这棵树进行计算,验证生成的 Merkle Root 是否和树自身的 Root 匹配;
上面两步通过后,就可以下载交易数据了, 对下载的每一笔交易数据可以求出它的 Txid, 然后验证 Txid 是否和 Merkle 树的叶子节点相匹配, 如果某个叶子节点没有匹配,可以单独下载这个叶子节点对应的交易,而不需要重新下载全部的交易.
场景二: SPV 节点验证区块中存在某笔交易
比特币网络是一个去中心化的网络,这个网络和我们日常生活中经常接触的网络有很大的不同,比如我们通过某个电商网站购买了一件商品, 我们购买这件商品的订单信息都存储在这个电商网站的数据库里, 假设我们要查询自己是否购买了这件商品,电商网站只需返回是或否就行了,当然实际的情况可能会返回这个订单的详情,但是本质是一样的. 也就是说在一个中心化的网络里,服务器是不需要向请求者证明自己响应的真实性,响应的真实性由自己的权威背书。比特币网络是一个去中心化的网络,它并没有一个权威中心,它对请求者的响应是需要自证真实性的. 假设 SPV 节点向比特币网络请求验证交易 Tx1 是否存在于区块中,这时候比特币网络不能简单地返回是或者否,如果 Tx1 不存在,可以返回否, 如果 Tx1 存在, 则要返回一支 Merkle 树的路径, SPV 节点可以通过这支 Merkle 路径自行验证交易是否存在, 这里的意思是: 我告诉你 Tx1 是存在的,并且你可以通过我发给你的 Merkle 路径验证我确实没有骗你.
画一张图说说什么是 Merkle 路径.
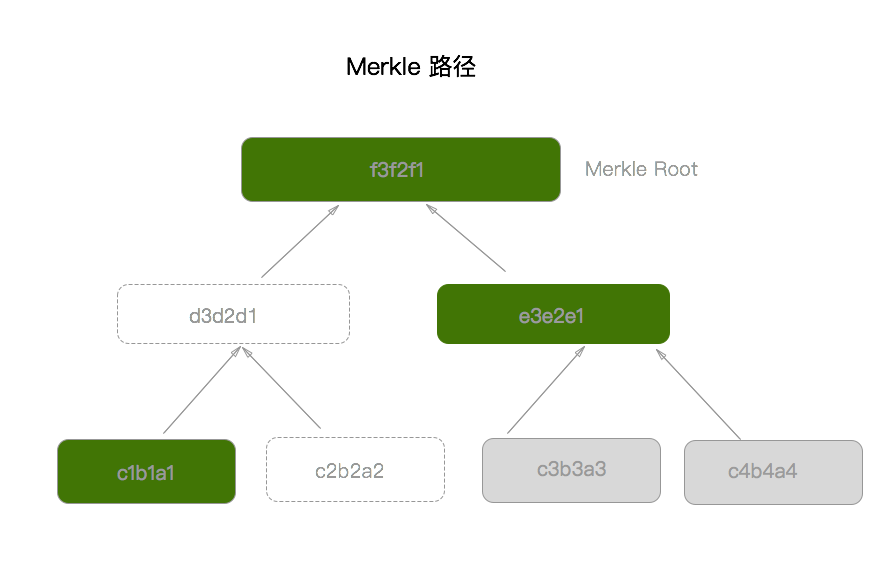
上图中绿色的部分表示 Merkle 树的一支路径,如果 SPV 节点向比特币网络请求验证交易 c2b2a2 是否存在于区块中,如果答案为是, 比特币网络会向 SPV 节点返回如上图的一支路径, SPV 节点接收到这支路径后会做如下两个工作:
-
验证路径上的 Merkle Root 是否和区块头链上对应区块的 Merkle Root 匹配;
-
第 1 步通过后, 将
c2b2a2和路径上的节点c1b1a1合并计算出节点d3d2d1, 将d3d2d1和路径上的节点e3e2e1合并计算出 Root 节点, 如果计算出的 Root 节点和路径上的 Root节点f3f2f1匹配,则验证成功;
上面两个场景的验证都是基于下面的定理, 并且受益于 Merkle 树, 如果只是简单的将所有交易合并然后计算 Hash 值是满足不了上面的两个场景的。
比特币区块链要么被破坏,但是不可被篡改
3.3.3 水到渠成, 生成我们自己的创世区块
我们在前面已经完成了下面的工作:
-
创建创世交易
-
为交易生成 Merkle 树
-
难度计算
将上面的三步工作组合起来,就可以生成创世区块了. 比特币创世区块的难度为 1 的 target 是: 0x1d00ffff, 这个难度对于我们家用的电脑还是有难度的, 如果想缩短生成创世区块的时间可以将其增大为: 0x1e00ffff 甚至 0x1f00ffff, 后者花的时间更短,如果使用后者, 创建区块的时间在我的家用电脑上大概是 10 秒, 详细的代码可以通过 kyk_gens_block.c 访问, 下面的代码只列出了 main() 函数的逻辑,
#include <stdio.h>
#include <stdlib.h>
#include <unistd.h>
#include <errno.h>
#include <string.h>
#include <time.h>
#include <openssl/pem.h>
#include "kyk_block.h"
#include "kyk_tx.h"
#include "kyk_sha.h"
#include "kyk_utils.h"
#include "kyk_script.h"
#include "kyk_address.h"
#include "kyk_mkl_tree.h"
#include "kyk_ser.h"
#include "kyk_difficulty.h"
#include "kyk_hash_nonce.h"
#define GENS_COINBASE "From 4/Sept/2017 China start suppressing the Bitcoin"
#define GENS_PEM "kyk-gens-priv.pem"
#define SC_PUBKEY_LEN 1000
#define KYK_TX_BUF_LEN 2000
#define KYK_BLK_LEN 1000 * 1000
#define KYK_BLK_HD_LEN 80
#define TX_COUNT 1
#define BLK_MAGIC_NO 0xD9B4BEF9
void create_gens_tx(struct kyk_tx *gens_tx);
char *make_address_from_pem(const char *pem_name);
void make_coinbase(struct kyk_txin *txin, const char *cb_note);
int get_priv_from_pem(uint8_t *priv, const char *pem_file_name);
struct kyk_mkltree_level *make_mkl_tree_root(struct kyk_tx_buf *buf_list, size_t len);
int main()
{
struct kyk_tx tx0;
uint8_t tx_buf[KYK_TX_BUF_LEN];
uint8_t hd_buf[KYK_BLK_HD_LEN];
uint8_t blk_buf[KYK_BLK_LEN];
uint8_t *blk_bfp = blk_buf;
size_t tx_len;
size_t wsize;
size_t hd_len;
size_t blk_len = 0;
struct kyk_hash *txid;
struct kyk_blk_header blk_hd;
struct kyk_tx_buf tx_buf_list[TX_COUNT];
struct kyk_tx_buf *tx_buf_ptr = tx_buf_list;
struct kyk_mkltree_level *mkl_root;
FILE *fp = fopen("kyk-gens-block.dat", "wb");
create_gens_tx(&tx0);
tx_len = kyk_seri_tx(tx_buf, &tx0);
tx_buf_ptr -> bdy = tx_buf;
tx_buf_ptr -> len = tx_len;
blk_hd.version = 1;
kyk_parse_hex(blk_hd.pre_blk_hash, "0000000000000000000000000000000000000000000000000000000000000000");
mkl_root = make_mkl_tree_root(tx_buf_ptr, TX_COUNT);
kyk_cpy_mkl_root_value(blk_hd.mrk_root_hash, mkl_root);
blk_hd.tts = 1504483200;
/* bts 越大,难度越低 */
blk_hd.bts = 0x1e00ffff;
blk_hd.nonce = 0;
kyk_hsh_nonce(&blk_hd);
hd_len = kyk_seri_blk_hd(hd_buf, &blk_hd);
/* 为了便于其他语言的解析程序解析 block 数据,没有序列化 magic-no 和 block-size */
//blk_len = kyk_inc_ser(&blk_bfp, "magic-no", BLK_MAGIC_NO);
//blk_len += kyk_inc_ser(&blk_bfp, "block-size", hd_len + tx_len + 1);
blk_len += kyk_inc_ser(&blk_bfp, "raw-buf", hd_buf, hd_len);
blk_len += kyk_inc_ser(&blk_bfp, "tx-count", TX_COUNT);
blk_len += kyk_inc_ser(&blk_bfp, "raw-buf", tx_buf, tx_len);
wsize = fwrite(blk_buf, sizeof(blk_buf[0]), blk_len, fp);
if(wsize == blk_len){
printf("saved gens block to kyk-gens-block.dat successfully\n");
}
txid = kyk_inver_hash((char *)tx_buf, tx_len);
kyk_print_hex("Txid ", txid -> body, txid -> len);
kyk_print_hex("Merkl Root ", blk_hd.mrk_root_hash, 32);
fclose(fp);
}
上面的代码从上到下,基本上是按照下面的步骤进行的:
-
创建创世交易
-
计算出 Merkle Root, 然后放到 block header 中
-
进行难度计算,算出 nonce, 这时候创世区块就已经做出来了
-
将创世区块写到文件中
编译运行程序:
$ make kyk_gens_block.c
$ ./kyk_gens_block.out
running...25300255
got block hash: 00000044481397b22e0fae24e230fe6d81b4ce94c6b7bfb124e29861484115c5
got nonce: 25300255
0x1e00ffff => target is: 0xffff000000000000000000000000000000000000000000000000000000
saved gens block to kyk-gens-block.dat successfully
Txid : b76d27da4abf50387dd70f5d6cc7e4df1d54722631cbbfdd292463df77aa0dbd
Merkl Root : b76d27da4abf50387dd70f5d6cc7e4df1d54722631cbbfdd292463df77aa0dbd
使用 ruby 解析刚生成的创世区块, parse_block.rb
./parse_block.rb kyk-gens-block.dat
{
"hash":"00000044481397b22e0fae24e230fe6d81b4ce94c6b7bfb124e29861484115c5",
"ver":1,
"prev_block":"0000000000000000000000000000000000000000000000000000000000000000",
"mrkl_root":"b76d27da4abf50387dd70f5d6cc7e4df1d54722631cbbfdd292463df77aa0dbd",
"time":1504483200,
"bits":503382015,
"nonce":25300255,
"n_tx":1,
"size":226,
"tx":[
{
"hash":"b76d27da4abf50387dd70f5d6cc7e4df1d54722631cbbfdd292463df77aa0dbd",
"ver":1,
"vin_sz":1,
"vout_sz":1,
"lock_time":0,
"size":145,
"in":[
{
"prev_out":{
"hash":"0000000000000000000000000000000000000000000000000000000000000000",
"n":4294967295
},
"coinbase":"04ffff001d01043446726f6d20342f536570742f32303137204368696e61207374617274207375707072657373696e672074686520426974636f696e"
}
],
"out":[
{
"value":"100.00000000",
"scriptPubKey":"OP_DUP OP_HASH160 0509ba514afa003a679ac7b6d7c2e2c96b37d5dc OP_EQUALVERIFY OP_CHECKSIG"
}
]
}
],
"mrkl_tree":[
"b76d27da4abf50387dd70f5d6cc7e4df1d54722631cbbfdd292463df77aa0dbd"
]
}
还可以用 hexdump 命令分析我们自己的创世区块,
$ hexdump -C kyk-gens-block.dat
00000000 01 00 00 00 00 00 00 00 00 00 00 00 00 00 00 00 |................|
00000010 00 00 00 00 00 00 00 00 00 00 00 00 00 00 00 00 |................|
00000020 00 00 00 00 bd 0d aa 77 df 63 24 29 dd bf cb 31 |.......w.c$)...1|
00000030 26 72 54 1d df e4 c7 6c 5d 0f d7 7d 38 50 bf 4a |&rT....l]..}8P.J|
00000040 da 27 6d b7 80 97 ac 59 ff ff 00 1e 1f 0d 82 01 |.'m....Y........|
00000050 01 01 00 00 00 01 00 00 00 00 00 00 00 00 00 00 |................|
00000060 00 00 00 00 00 00 00 00 00 00 00 00 00 00 00 00 |................|
00000070 00 00 00 00 00 00 ff ff ff ff 3c 04 ff ff 00 1d |..........<.....|
00000080 01 04 34 46 72 6f 6d 20 34 2f 53 65 70 74 2f 32 |..4From 4/Sept/2|
00000090 30 31 37 20 43 68 69 6e 61 20 73 74 61 72 74 20 |017 China start |
000000a0 73 75 70 70 72 65 73 73 69 6e 67 20 74 68 65 20 |suppressing the |
000000b0 42 69 74 63 6f 69 6e ff ff ff ff 01 00 e4 0b 54 |Bitcoin........T|
000000c0 02 00 00 00 19 76 a9 14 05 09 ba 51 4a fa 00 3a |.....v.....QJ..:|
000000d0 67 9a c7 b6 d7 c2 e2 c9 6b 37 d5 dc 88 ac 00 00 |g.......k7......|
000000e0 00 00 |..|
000000e2
现在我们终于拥有了一块属于自己掌控的创世区块. 可以调控 blk_hd.bts = 0x1e00ffff 来调整区块的生成耗时, blk_hd.bts 越大耗时越短.
4. 参考文档和补充说明
4.1 参考文档
[1] https://en.bitcoin.it/wiki/Main_Page, Bitcoin Wiki
[2] https://webbtc.com/, 可以下载 json, hex, binary 三种格式的比特币数据
[3] https://en.bitcoin.it/wiki/Block_hashing_algorithm, Block hashing algorithm
[4] https://en.bitcoin.it/wiki/Difficulty, 比特币挖矿难度
[5] https://en.wikipedia.org/wiki/Proof-of-work_system Proof-of-work system
[6] https://en.wikipedia.org/wiki/Client_Puzzle_Protocol Client Puzzle Protocol
[7] https://en.bitcoin.it/wiki/Hashcash Hashcash
[8] https://en.bitcoin.it/wiki/Protocol_documentation#Merkle_Trees Merkle Trees
[9] https://en.bitcoin.it/wiki/Block Block 的结构
[10] https://en.bitcoin.it/wiki/Protocol_rules#.22block.22_messages Protocol rules 涉及到了 Tx 和 Block 的验证规则
[11] https://en.bitcoin.it/wiki/Genesis_block Genesis block 创世区块
[12] https://en.bitcoin.it/wiki/Target Target
[13] https://gmplib.org/manual/ GNU MP
[14] GMP Integer Import and Export
[15] https://99bitcoins.com/2016-bitcoin-mining-hardware-comparison/ 比特币矿机行话
[16] https://en.wikipedia.org/wiki/Names_of_large_numbers Names of large numbers
[17] https://stackoverflow.com/questions/12791864/c-program-to-check-little-vs-big-endian Little Endian 和 Big Endian
[18] https://en.wikipedia.org/wiki/Endianness Endianness
[19] https://github.com/bitcoinbook/bitcoinbook/blob/second_edition/ch09.asciidoc ch09 of Mastering Bitcoin
[20] https://en.bitcoin.it/wiki/Technical_background_of_version_1_Bitcoin_addresses Bitcoin Address
[21] https://en.bitcoin.it/wiki/Transaction#Pay-to-PubkeyHash Pay To PubkeyHash
[22] https://en.bitcoin.it/w/index.php?title=Scalability&redirect=no#Simplified_payment_verification Simplified payment verification
[23] http://www.samlewis.me/2017/06/a-peek-under-bitcoins-hood/ A peek under Bitcoin’s hood
[24] https://github.com/ElementsProject/lightning c-lightning — a Lightning Network implementation in C
[25] https://github.com/keeshux/basic-blockchain-programming Sample code from blog series “Basic blockchain programming”
[26] http://davidederosa.com/basic-blockchain-programming/ A developer-oriented series about Bitcoin in basic blockchain programming
[27] https://en.bitcoin.it/wiki/Block_timestamp Block timestamp
[28] https://en.bitcoin.it/wiki/Script#Constants Script Constants
[29] 区块链技术探索(二), 打造我们自己的比特币 这里构造了一个可以在自己电脑上运行的实验型的比特币系统
4.2 补充说明
1. 为什么比特币使用 Double Hash ?
来源于: https://en.bitcoin.it/wiki/Hashcash
Bitcoin is using two hash iterations (denoted SHA256^2 ie “SHA256 function squared”) and the reason for this relates to a partial attack on the smaller but related SHA1 hash. SHA1’s resistance to birthday attacks has been partially broken as of 2005 in O(2^64) vs the design O(2^80), with practical attacks having been used successfully in early 2017. While hashcash relies on pre-image resistance and so is not vulnerable to birthday attacks, a generic method of hardening SHA1 against the birthday collision attack is to iterate it twice. A comparable attack on SHA256 does not exist so far, however as the design of SHA256 is similar to SHA1 it is probably defensive for applications to use double SHA256. And this is what bitcoin does, it is not necessary given hashcash reliance on preimage security, but it is a defensive step against future cryptanalytic developments. The attack on SHA1 and in principle other hashes of similar design like SHA256, was also the motivation for the NIST SHA3 design competition which is still ongoing.
简单地说就是比特币使用 Double Hash 是为了防御 birthday attacks.
2. 比特币系统中的字节序(endian)[17] 问题
Suppose we are on a 32-bit machine, then int x = 1
If it is little endian, the x in the memory will be something like:
higher memory
----->
+----+----+----+----+
|0x01|0x00|0x00|0x00|
+----+----+----+----+
A
|&x
so *(char*)(&x) == 1
If it is big endian, it will be:
+----+----+----+----+
|0x00|0x00|0x00|0x01|
+----+----+----+----+
A
|&x
so *(char*)(&x) == 0
比特币中绝大部分的数据是以 Little-Endian 形式存储的, 我在第1节的文章中描述解析交易的时候经常直接使用 fread 读取数据, 比如:
int main()
{
FILE *fp;
unsigned int tx_version;
fp = fopen("tx0.bin", "rb");
fread(&tx_version, sizeof(tx_version), 1, fp);
printf("Tx Version: %u\n", tx_version);
}
如果我们的机器本身是 Big-Endian 形式的那么上面的代码就会解析出一个错误的 tx_version, 如果是机器是 Little-Endian 形式,那么程序可以解析出正确的 tx_version, 由于我们大部分的家用电脑使用的是 Intel CPU, 而 Intel CPU 都是 Little-Endian [18], 所以上面的解析程序在我们自用的电脑上还是可以正常运行的, 如果考虑到跨平台运行,就一定要考虑到目标主机的 Endianness.
3. Merkle Root 和 Txid 字节序的处理方法
Merkle Root 和 Txid 都是对目标数据进行两次 SHA256 计算得到的一个倒序结果,用公式表达就是: 1. result = SHA256(SHA256(data)), 2. 通过 reverse_bytes(result) 得到 Merkle Root 或者 Txid
在序列化 Merkle Root 或者 Txid 时又需要将 Merkle Root 或者 Txid 倒序过来比如: reverse_bytes(Merkle Root) 或者 reverse_bytes(Txid), 在序列化 block header 时就是这样处理的, 相关的代码在: kyk_block.c, 其中的
kyk_reverse_pack_chars 就是用来对数据进行倒序形式的序列化的。貌似比特币中所有的通过 hash(即两次 SHA256 计算) 运算的结果都使用和 Merkle Root, Txid 相同的字节序处理方法。
size_t kyk_seri_blk_hd(uint8_t *buf, const struct kyk_blk_header *hd)
{
size_t len = 0;
size_t total = 0;
len = beej_pack(buf, "<L", hd -> version);
buf += len;
total += len;
len = kyk_reverse_pack_chars(buf, (unsigned char *)hd -> pre_blk_hash, sizeof(hd -> pre_blk_hash));
buf += len;
total += len;
len = kyk_reverse_pack_chars(buf, (unsigned char *)hd -> mrk_root_hash, sizeof(hd -> mrk_root_hash));
buf += len;
total += len;
len = beej_pack(buf, "<L", hd -> tts);
buf += len;
total += len;
len = beej_pack(buf, "<L", hd -> bts);
buf += len;
total += len;
len = beej_pack(buf, "<L", hd -> nonce);
buf += len;
total += len;
return total;
}
size_t kyk_seri_blk_hd_without_nonce(uint8_t *buf, const struct kyk_blk_header *hd)
{
size_t len = 0;
size_t total = 0;
len = beej_pack(buf, "<L", hd -> version);
buf += len;
total += len;
len = kyk_reverse_pack_chars(buf, (unsigned char *)hd -> pre_blk_hash, sizeof(hd -> pre_blk_hash));
buf += len;
total += len;
len = kyk_reverse_pack_chars(buf, (unsigned char *)hd -> mrk_root_hash, sizeof(hd -> mrk_root_hash));
buf += len;
total += len;
len = beej_pack(buf, "<L", hd -> tts);
buf += len;
total += len;
len = beej_pack(buf, "<L", hd -> bts);
buf += len;
total += len;
return total;
}