计算竞彩足球注数

竞彩足球的注数是由选号方式和过关方式确定的，为了便于描述，我以竞彩足球的胜平负，过关投注, 同时去掉让球数为例子进行展开，至于什么是胜平负，什么是让球数我在这里就不解释了。假设我选择了三场比赛 [C1, 胜], [C2, 负], [C3, 平], [C1, 胜]的意思是: C1比赛，我选择主队胜, 我们要知道竞彩足球里的胜负平都是针对主队来说的，[C2, 负] 表示 C2比赛主队负, [C3, 平] 表示C3比赛主客平, 这样我们就完成了一次选号, 进一步我们可以为这个选号定义数据结构, 在 ruby 中的实现如下, 我们把这个选号方式记做为 C,

 [
   ['C1', 3],
   ['C2', 1],
   ['C3', 0]
 ]

3 表示主队胜, 1 表示主队负, 0 表示主客平。接下来我们选择过关方式, 首先我们看一张图, 此图叫做过关投注图,

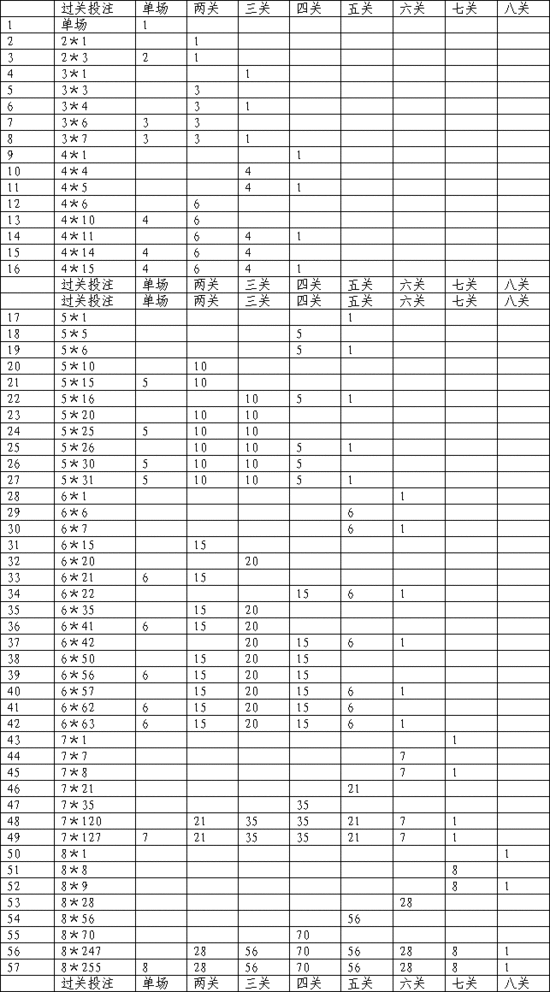
单场也叫单关, 即一场比赛的竞猜为一注, [‘C1’, 3] 为一个单关

两关, 即两场比赛的竞猜为一注, [‘C1’, 3] 和 [‘C2’, 1] 组合起来为一个两关, [‘C1’, 3] 和 [‘C3’, 0] 组合起来为一个两关, [‘C2’, 1] 和 [‘C3’, 0] 组合起来也为一个两关

三关, 即三场比赛的竞猜为一注, [‘C1’, 3], [‘C2’, 1], [‘C3’, 0] 三者组合起来为一个三关

四到八关的定义类似

由过关投注图, 我们可以知道选号 C 的过关方式可以为: 单场, 2串1, 2串3, 3串1, 3串3, 3串4, 3串6, 3串7, 现在我们来计算选号 C 在不同过关方式下的注数，所谓的注数其实就是过关集合的大小，于是计算注数，变成了求过关集合。

选择单场, 过关集合由单关组成, 集合大小为 3, 因而此时注数为 3
```
  [['C1', 3], ['C2', 1], ['C3', 0]]
```

选择2串1, 过关集合由两关组成, 集合大小为 3, 因而此时注数为 3

  [
    [["C1", 3], ["C2", 1]],
    [["C1", 3], ["C3", 0]],
    [["C2", 1], ["C3", 0]]
  ]

选择2串3, 过关集合由单关和两关组成, 集合大小为 6, 其中单关和双关各3个, 因而此时注数为 6

[
  [["C1", 3], ["C2", 1]],
  [["C1", 3], ["C3", 0]],
  [["C2", 1], ["C3", 0]],
  [["C1", 3]],
  [["C2", 1]],
  [["C3", 0]]
]

3串1, 3串3, 3串4, 3串6, 3串7 等过关方式的解法类似，我们重点看下 3串4的解法,

选择3串4, 过关集合由两关和三关组成, 集合大小为 4, 其中两关 3 个, 三关 1个, 因而此时注数为 4

  [
    [["C1", 3], ["C2", 1]],
    [["C1", 3], ["C3", 0]],
	[["C2", 1], ["C3", 0]],
	[["C1", 3], ["C2", 1], ["C3", 0]]
  ]

从过关投注图中，我们可以看到 3*4(即3串4) 那一行有数字 3 在两关列，数字 1 在三关列，我们可以忽略这些数字的大小，这些数字的意义就是告诉我们过关方式3串4是由两关和三关组成，其他过关方式的构造也可以由此方法得到。于是我们可以得到一张表用来表示各个过关方式的结构，用 ruby 代码可以表示为,

BET_TABLE = {
  '1*1'=>[1],
  '2*1'=>[2],
  '2*3'=>[2, 1],
  '3*1'=>[3],
  '3*3'=>[2],
  '3*4'=>[2,3],
  '3*7'=>[3, 2, 1],
  '4*1'=>[4],
  '4*4'=>[3],
  '4*5'=>[4,3],
  '4*6'=>[2],
  '4*11'=>[2, 3, 4],
  '4*15'=>[4, 3, 2, 1],
  '5*1'=>[5],
  '5*5'=>[4],
  '5*6'=>[5, 4],
  '5*10'=>[2],
  '5*16'=>[5, 4, 3],
  '5*20'=>[3, 2],
  '5*26'=>[5, 4, 3, 2],
  '5*31'=>[5, 4, 3, 2, 1],
  '6*1'=>[6],
  '6*6'=>[5],'6*7'=>[6, 5],
  '6*15'=>[2],
  '6*20'=>[3],
  '6*22'=>[6, 5, 4],
  '6*35'=>[3,2],
  '6*42'=>[6, 5, 4, 3],
  '6*50'=>[4, 3, 2],
  '6*57'=>[6, 5, 4, 3, 2],
  '6*63'=>[6, 5, 4, 3, 2, 1],
  '7*1'=>[7],
  '7*7'=>[6],
  '7*8'=>[7,6],
  '7*21'=>[5],
  '7*35'=>[4],
  '7*120'=>[7,6,5,4,3,2],
  '8*1'=>[8],
  '8*8'=>[7],
  '8*9'=>[8,7],
  '8*28'=>[6],
  '8*56'=>[5],
  '8*70'=>[4],
  '8*247'=>[8,7,6,5,4,3,2],
  '9*1'=>[9],
  '10*1'=>[10],
  '11*1'=>[11],
  '12*1'=>[12],
  '13*1'=>[13],
  '14*1'=>[14],
  '15*1'=>[15]
}

'1*1' => [1] 表示 1串1 由单关组成, '2*3' => [2, 1] 表示 2串3 由两关和单关组成，'3*4' => [2,3] 表示 3串4 由二关和三关组成, 其他元素的意义类似。

我们开始用 ruby 程序来计算注数,

  teams = [
   ['C1', 3],
   ['C2', 1],
   ['C3', 0]
  ]
  play_kind = "3*4"

  def combination(num, teams)
    teams.combination(num).to_a
  end

  def get_bet_collection(play_kind, teams)
    BET_TABLE[play_kind].flat_map {|num|
      combination(num, teams)
    }
  end

  bet_collection = get_bet_collection play_kind, teams

  # 注数
  betsum = bet_collection.size

代码非常简单, teams 表示选号方式, play_kind 表示过关方式, combination(num, teams) 用于计算 teams 的过关集合, 比如 combination(2, teams) 可以计算出 teams 的两关集合, combination(3, teams)可以计算出 teams 的三关集合, 于是 combination(2, teams) 和 combination(3, teams) 的合集就是我们需要的3串4的过关集合, 方法 get_bet_collection 的实现原理即如此。

现在我们考虑一种稍微复杂点的情况,

  teams =  [
   ['C1', 3,1,0],
   ['C2', 1,3],
   ['C3', 0,1]
   ]
  play_kind = "3*4"

  def combination(num, teams)
    teams.combination(num).to_a
  end

  def get_bet_collection(play_kind, teams)
    BET_TABLE[play_kind].flat_map {|num|
      combination(num, teams)
    }
  end

  bet_collection = get_bet_collection play_kind, teams

选号方式 teams 变得稍微复杂了点, [‘C1’, 3, 1, 0] 可以拆成 [‘C1’, 3], [‘C1’, 1] 和 [‘C1’, 0];

[‘C2’, 1, 3] 可以拆成 [‘C2’, 1] 和 [‘C2’, 3];

[‘C3’, 0, 1] 可以拆成 [‘C3’, 0] 和 [‘C3’, 1]。

于是我们增加一个方法,

  def split_teams_to_single_teams teams
    single_teams = []
    teams.each {|team|
      team[1..-1].uniq.each {|st|
        single_teams << [team[0], st]
      }
    }
	single_teams
  end

调用 split_teams_to_single_teams teams 可以得到:

single_teams = [
                 ["C1", 3],
				 ["C1", 1],
				 ["C1", 0],
				 ["C2", 1],
				 ["C2", 3],
				 ["C3", 0],
				 ["C3", 1]
			  ]

问题来了，[“C1”, 3], [“C1”, 1] 和 [“C1”, 0] 这类属于同一场比赛的单关是不允许组合起来成为二关，三关等多关，比如 [[“C1”, 3], [“C1”, 1]]这种组合是不允许的。因此我们需要在过关集合中把这类元素去掉，于是我们对 combination 方法进行修改, 结果如下,

  def combination(num, teams)
    teams.combination(num).to_a.delete_if {|team|
	  tnames = team.map {|t| t[0]}
	  tnames.size > tnames.uniq.size
	}
  end

从而我们就能把那些由同一场比赛的单关组合成的元素去掉。最后我们的程序如下,

  def combination(num, teams)
	teams.combination(num).to_a.delete_if {|team|
	  tnames = team.map {|t| t[0] }
	  tnames.size > tnames.uniq.size
	}
  end

  def get_bet_collection(play_kind, teams)
    BET_TABLE[play_kind].flat_map {|num|
      combination(num, teams)
    }
  end

  def split_teams_to_single_teams teams
    single_teams = []
    teams.each {|team|
      team[1..-1].uniq.each {|st|
        single_teams << [team[0], st]
      }
    }
    single_teams
  end

  teams = [
   ['C1', 3,1,0],
   ['C2', 1,3],
   ['C3', 0,1]
   ]
  play_kind = "3*4"

  single_teams = split_teams_to_single_teams teams
  bet_collection = get_bet_collection play_kind, single_teams

  # 注数
  betsum = bet_collection.size
  puts bet_collection.inspect
  puts betsum

我们计算出 bet_collection 是,

[
  [["C1", 3], ["C2", 1]],
  [["C1", 3], ["C2", 3]],
  [["C1", 3], ["C3", 0]],
  [["C1", 3], ["C3", 1]],
  [["C1", 1], ["C2", 1]],
  [["C1", 1], ["C2", 3]],
  [["C1", 1], ["C3", 0]],
  [["C1", 1], ["C3", 1]],
  [["C1", 0], ["C2", 1]],
  [["C1", 0], ["C2", 3]],
  [["C1", 0], ["C3", 0]],
  [["C1", 0], ["C3", 1]],
  [["C2", 1], ["C3", 0]],
  [["C2", 1], ["C3", 1]],
  [["C2", 3], ["C3", 0]],
  [["C2", 3], ["C3", 1]],
  [["C1", 3], ["C2", 1], ["C3", 0]],
  [["C1", 3], ["C2", 1], ["C3", 1]],
  [["C1", 3], ["C2", 3], ["C3", 0]],
  [["C1", 3], ["C2", 3], ["C3", 1]],
  [["C1", 1], ["C2", 1], ["C3", 0]],
  [["C1", 1], ["C2", 1], ["C3", 1]],
  [["C1", 1], ["C2", 3], ["C3", 0]],
  [["C1", 1], ["C2", 3], ["C3", 1]],
  [["C1", 0], ["C2", 1], ["C3", 0]],
  [["C1", 0], ["C2", 1], ["C3", 1]],
  [["C1", 0], ["C2", 3], ["C3", 0]],
  [["C1", 0], ["C2", 3], ["C3", 1]]
 ]

我们看到集合由 16 个二关和 12 个三关组成, 因此注数是 28 注。